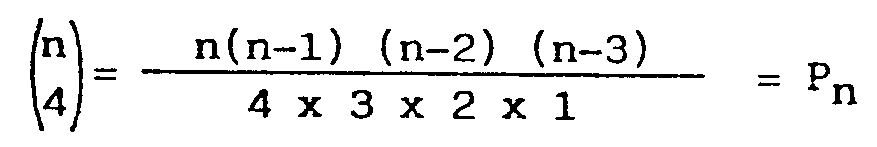NUMEROS EN POLIGONOS
Un polígono
convexo es aquél que no tiene entrantes, es decir, está todo
él al mismo lado de cada uno de sus bordes. Un triángulo
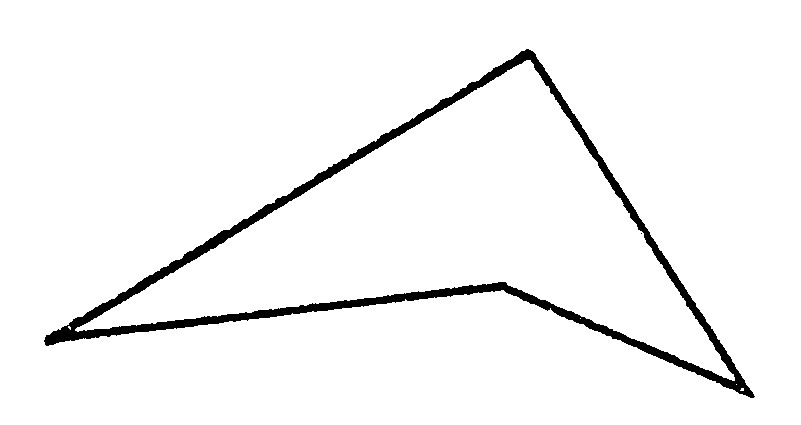
es un polígono convexo, un cuadrado también, pero este cuadrilátero
no lo es
La suma de
los ángulos de un triángulo es de 180º. La suma de los
ángulos de un cuadrado o de un rectangulo es de 4x90º=360º=2x180º.
¿Será 180 un número mágico para esto de los
ángulos? ¿Cuánto vale la suma de los ángulos
de un pentágono convexo o de un polígono convexo de n lados?
Constrúyete
un pentágono, mide con tu transportador de ángulos y suma.
¿Te sale más o menos 540º? Entonces has medido bien.
Observa que 540º= 3 x 180º. De nuevo el 180 por medio.
¿Por qué tendrá que ser así? Fíjate
cómo van las cosas. Vamos a tratar de medir la suma de los ángulos
exteriores, es decir, de los señalados en la figura siguiente
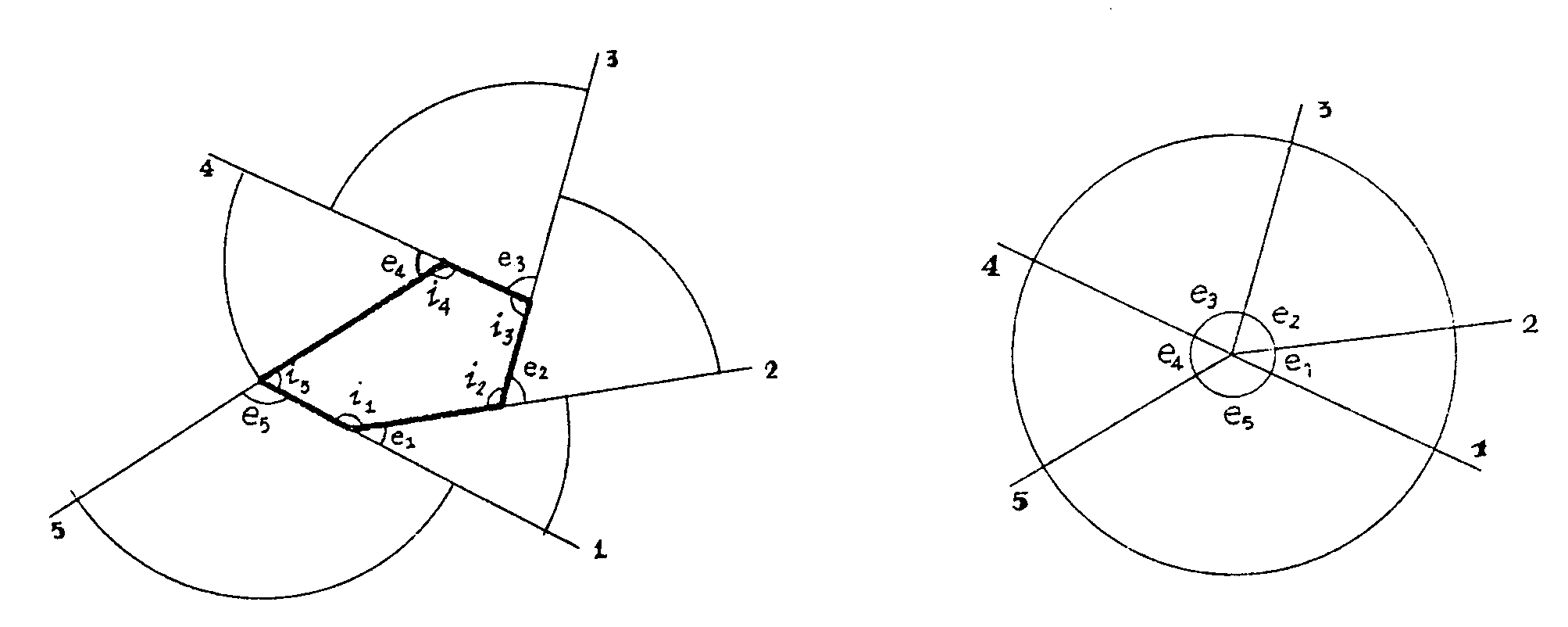
Con un compás y con radio 2 cm. señala
bien los arcos cuya suma quieres medir. Observa. Si trasladas paralelamente
todos los arcos hasta tener su centro en un mismo punto 0, está
claro que cada uno empieza donde el otro termina y que entre todos forman
una circunferencia entera. Así resulta que la suma de todos los
ángulos exteriores es 360º=2x180º. Y esto va a
ser así también, haciendo lo mismo, cualquiera que sea el
número de lados del polígono convexo que consideremos.
¿Cuál
será ahora la suma de los ángulos interiores en el caso del
pentágono? Es decir, ¿cuánto vale i1+i2+i3+i4+i5=Si?
Observa que i1+e1=180º
y así i1=180º-e1.
Por tanto i1+i2+i3+i4+i5=5x180º-(e1+e2+e3+e4+e5)=5x180º-2x180º=(5-2)x180º
Y exactamente del mismo modo, si tienes un polígono
convexo de n lados, resulta que la suma de los ángulos exteriores
es de 2x180º y la suma de los ángulos interiores es
de (n-2)x180º.
Vamos a hacer
más números. ¿Cuántas diagonales hay
en un polígono convexo? En un triángulo ninguna.
En un cuadrado 2, en un rectángulo 2, en un pentágono convexo
5, en un exágono convexo 9, en un polígono convexo de 10
lados... muchísimas ¿no? Trazarlas y contarlas es un rollo.
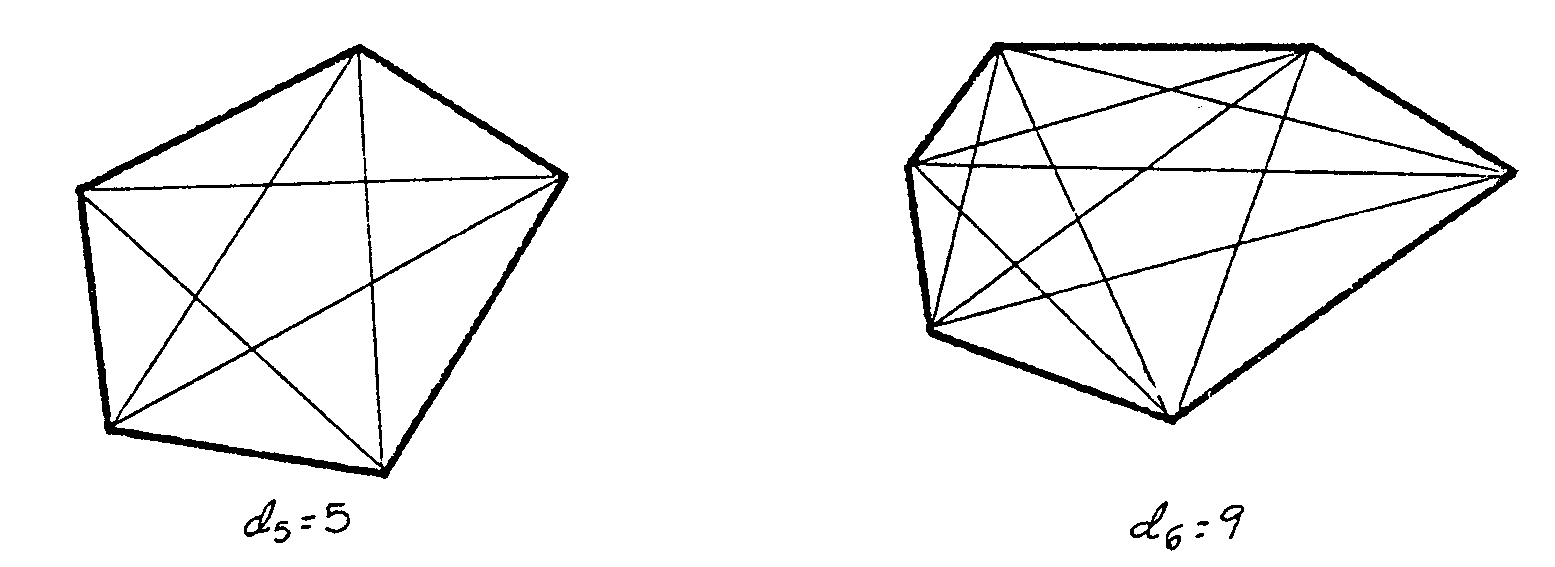
Vamos a ver si podemos averiguar sin contar. ¿Cuántas
salen de cada vértice V de un polígono de 10 lados? Es claro
que los segmentos que van a vértices distintos de V y que no son
adyacentes son los que nos dan las diagonales. Adyacentes hay 2 y así
las diagonales que salen de V son 10-3=7. ¿Quiere esto decir que
habrá 70 diagonales? Parecen muchas ¿no? Si por cada vértice
contamos 7, entonces cada diagonal queda contada dos veces, una por cada
vértice que la diagonal une. Así resulta que el número
de diagonales es la mitad de 70, es decir, 35. Hay 35 diagonales en el
decágono convexo. ¿Y en el polígono convexo de n lados?
Ahora ya sabes lo que hay que hacer. El número de diagonales será
n(n-3)/2=dn
Comprueba que efectivamente si n=3, d3=0;
si n=4, d4=2; n=5, d5=5....Sin
necesidad de contar sabemos que si n=20, d20=170.
Otra cuenta
interesante. Tienes un polígono convexo de n lados. Supongamos que
al trazar las n(n-3)/2 diagonales no hay tres que pasan por un mismo punto
que no sea vértice. ¿Cuál es el número
de puntos interiores que quedan determinados por intersección de
las diagonales?
Vamos a contar un poco, pintando
n=4  P4=1
n=5
P4=1
n=5 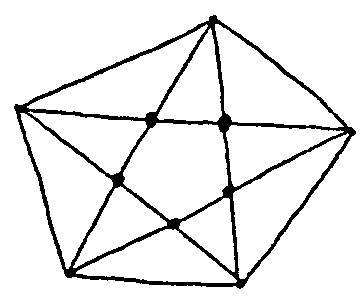 P5=5
n=6
P5=5
n=6 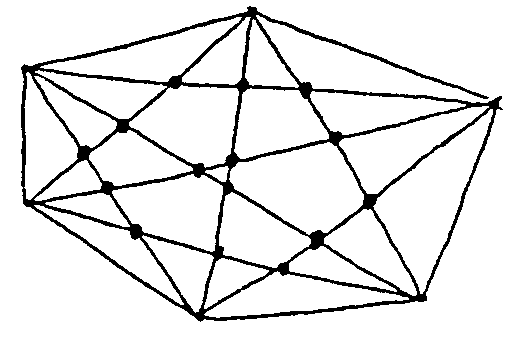 P6=15
n=7
me pierdo
P6=15
n=7
me pierdo
Vamos a tratar
de pensar un poco. Cada punto interior, interior, intersección de
dos diagonales ¿cómo queda determinado? naturalmente que
por las dos diagonales que se cortan en él. ¿Y estas diagonales?
Cada una por los dos vértices que une. Así para cada cuatro
vértices A,B,C,D, que escojamos de nuestro polígono, estén
donde estén, aunque al unirlos obtenemos seis rectas AB, AC, AD,
BC, CD, sólo dos de ellas se cortan en el interior del polígono,
las otras se cortan fuera o en el borde. Así cada cuatro vértices
determinan un sólo punto interior y cada punto interior intersección
de dos diagonales corresponde a un solo grupo de 4 vértices. Así
es claro que hay tantos puntos interiores de intersección como grupos
diferentes de cuatro vértices se puedan formar. ¿Cuántos
de estos grupos hay? Elemental:
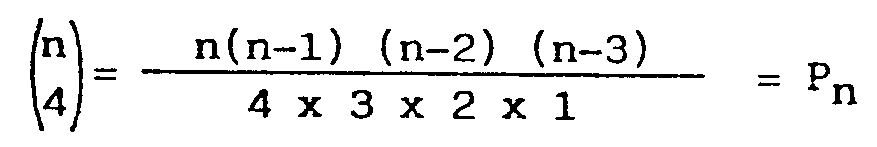
Haciendo cuentas para comprobar resulta P4=1,
P5=5, P6=15,
P7=35. Como ves, un contar con astucia,
sin contar uno a uno, ahorra un montón de trabajo aburrido.







 P4=1
P4=1 P5=5
P5=5 P6=15
P6=15