LAS PITAGÓRICAS MARAVILLAS DEL PENTAGONO
REGULAR.
El pentágono
regular es una de las figuras con más miga de toda la historia antigua
de la matemática. Si trazas sus diagonales obtienes el pentagrama
pitagórico, la figura que los seguidores de Pitágoras utilizaban
en el siglo VI a. de C. para reconocimiento mutuo y como símbolo
de salud.
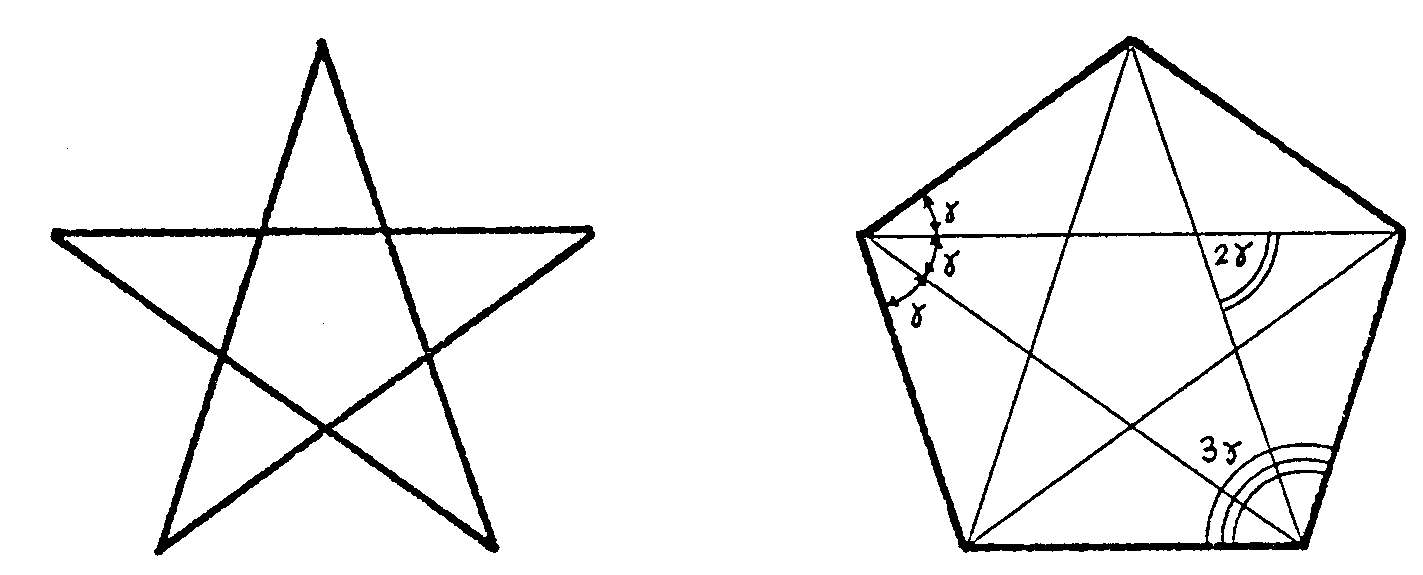
Al formar
la estrella pitagórica, en el centro se forma otro pentágono
regular. Si mides los ángulos que se forman en el pentágono
señalados en la figura anterior observarás una cosa curiosa:
si por abreviar llamas 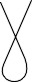 al ángulo de 36º resulta que todos los ángulos que aparecen
miden un múltiplo entero de
al ángulo de 36º resulta que todos los ángulos que aparecen
miden un múltiplo entero de 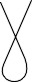 ,
como está indicado.
,
como está indicado.
A los pitagóricos,
que eran grandes devotos de las proporciones exactas, esto les tuvo que
sumir en un profundo éxtasis y de ahí su veneración
por el pentagrama. Y esta misma idea de tratar de encontrar proporciones
exactas entre magnitudes geométricas les llevó por primera
vez, como sospechan los historiadores de la matemática, mediante
el pentágono regular precisamente, a uno de los descubrimientos
matemáticos más importantes, el de la inconmensurabilidad
de ciertos segmentos. Verás en qué consiste esto.
Era natural
para los pitagóricos esperar que en una figura tan perfectísima
como el pentágono regular, el lado l y la diagonal d
fuesen conmensurables, es decir, que admitiesen una unidad de medida común,
o en otras palabras, que existiese un segmento u más pequeño
que d y l con el que l y d se pudieran medir
a la vez, es decir, que d resultase ser m veces u
y l fuese n veces u, siendo m y n números
enteros.
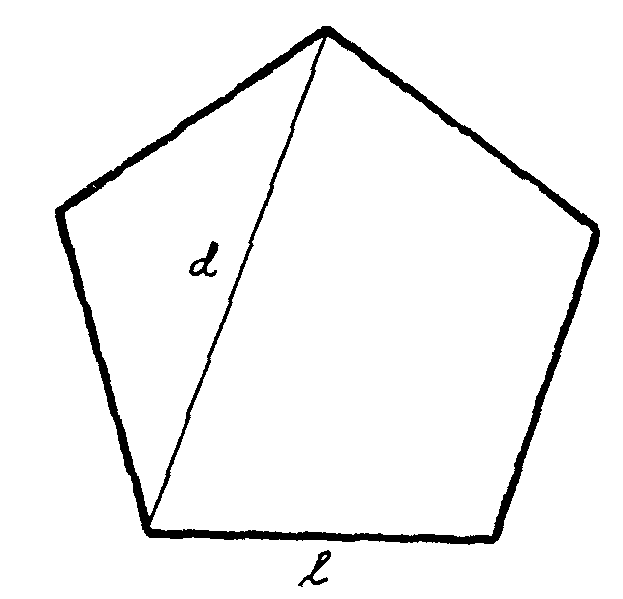 ¿Ocurrirá
que d = mu, l = nu siendo m y
n números enteros?
¿Ocurrirá
que d = mu, l = nu siendo m y
n números enteros?
Si m/n
no fuese una fracción irreducible, por ejemplo, m=m´p,
n=n´p, entonces es claro quqe podemos tomar como segmento
unidad U=pu y con esta unidad resulta que d mide m´
veces U y l mide n´ veces U, es decir
U sirve también para medir d y l. Si todavía
m´ y n´ tuviesen un factor común, podríamos
tomar una unidad más grande. Como ves, si existe una unidad u
que sirve para medir a la vez d y l en enteros, también
existe una unidad U* que sirve para medir d y l con
m* y n* tales que m*/n* es una fracción irreducible.
Supongamos que existe tal u y que hemos tomado U* por unidad.
Así d mide m*U* y l mide n*U*, siendo
m*/n* irreducible.
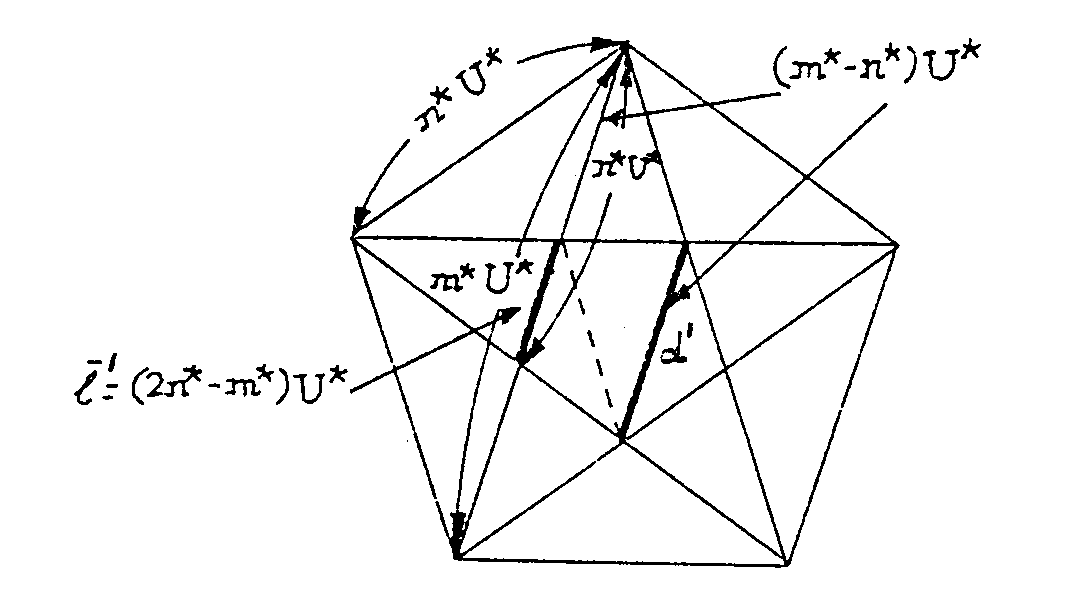
Pero ahora
fácilmente, apoyándote en lo que sabes sobre los ángulos
de la figura del pentágono y sus diagonales, observarás que
las medidas de los segmentos indicados en la figura siguiente son las señaladas,
en particular que la diagonal d´ del pentágono regular
interior resulta ser (m*-n*) U* y el lado l´ del mismo
pentágono interior es (2n*-m*) U*. Como dos pentágonos
regulares cualesquiera son semejantes, resulta que d/l= d´l´
y, por tanto, m*/n* = (m*-n*)/(2n*-m*), lo cual quiere decir que
m*/n* no era irreducible, contra lo que habíamos supuesto.
Algo no casa. ¿Qué puede ser? Nuestro razonamiento
es bueno. Entonces nuestro punto de partida tiene que ser malo. Habíamos
partido de que existe u tal que d=mu, l=nu. Esto tiene
que ser falso. En resumen, d y l no pueden ser conmensurables,
es decir, no se puede encontrar una unidad u con la que se pueda medir
a la vez d y l en números enteros.
La relación
en la que se encuentran la diagonal y el lado del pentágono regular
se puede obtener de nuestras cuentas anteriores. Tenemos que se verifica
d/l=m/n y aunque ya sabemos ahora que m y n no pueden
ser enteros a la vez, sabemos que d/l=m/n=(m-n)/(2n-m). Así,
llamando x=m/n resulta x=m/n=(x-1)/(2-x). Por lo tanto, x2-x-1=0,
es decir x =  = 1,618..., un número que ya hemos conocido antes y que tiene que
ver con la sección áurea de un segmento, como vas a ver ahora.
= 1,618..., un número que ya hemos conocido antes y que tiene que
ver con la sección áurea de un segmento, como vas a ver ahora.
Como puedes
observar en la figura siguiente,
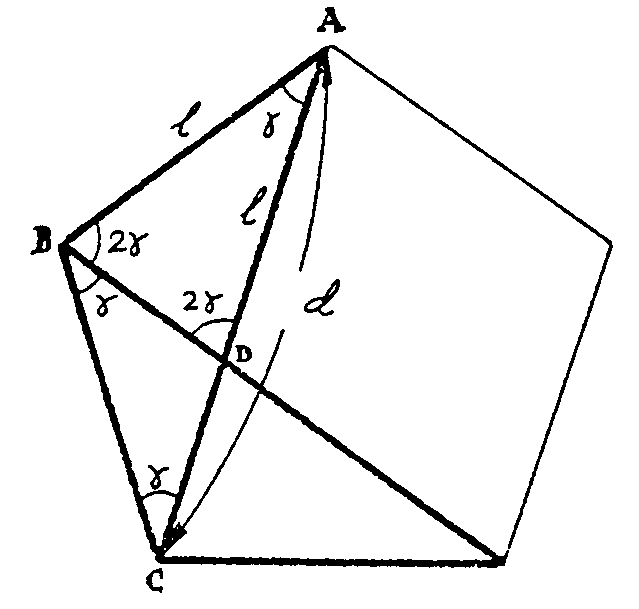
resulta que los triángulos ABC y BDC son semejantes
y así AC/AD=AC/AB=BC/DC, es decir, d/l=1/(d-l),
lo que quiere decir que AD, que es igual al lado, es sección áurea
de la diagonal, lo cual, añadía otro encanto más del
pentágono regular para los ojos pitagóricos. En realidad,
con un poco más de esfuerzo, puedes comprobar que en el pentagrama
y pentágono regular, cualquier segmento es sección áurea
del que es inmediatamente mayor.





 ¿Ocurrirá
que d = mu, l = nu siendo m y
n números enteros?
¿Ocurrirá
que d = mu, l = nu siendo m y
n números enteros?

