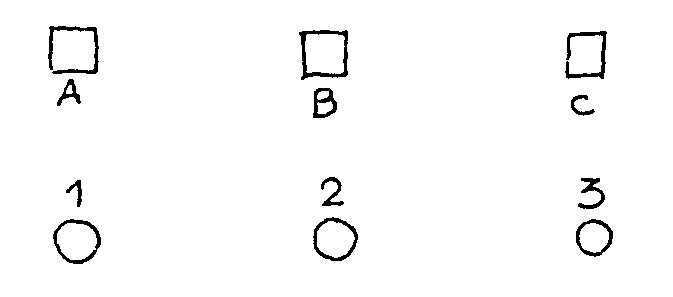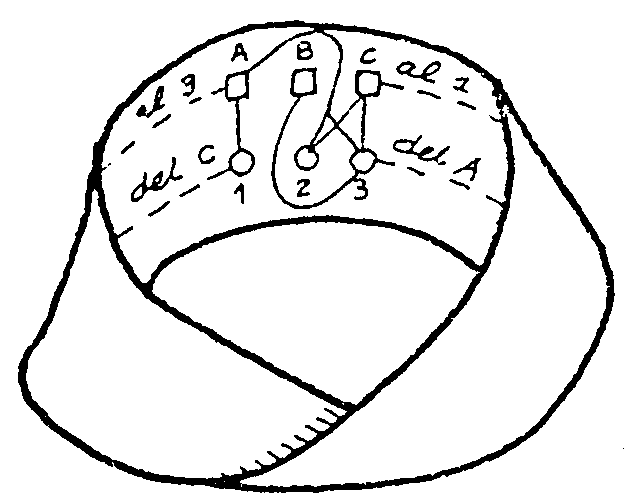UNA CINTA MÁGICA
Te propongo
un problema. Dados cuatro puntos en el plano A,B,C,D, unir cada uno a los
otros tres mediante líneas rectas o curvas del plano que no se crucen.
Cada línea debe contener sólo dos de los puntos. Piensa.
Fácil ¿no?
Ahora un poco
más difícil. Dados cinco puntos en el plano, unir cada uno
a los otros cuatro por líneas que no se crucen.
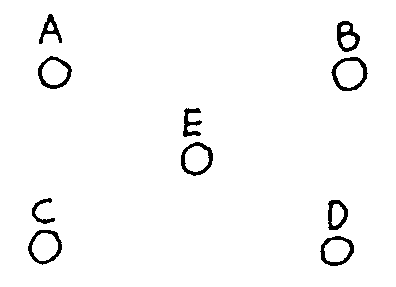
Prueba un rato. Parece más difícil ¿no?...
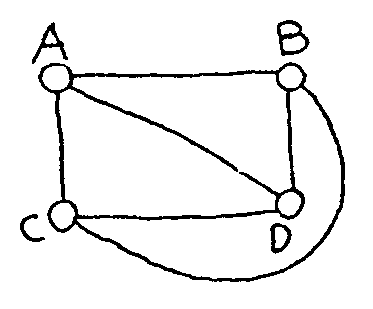
Yo diría más aún: ¡Imposible! Fijate: si colocas
cuatro puntos A,B,C,D, los puedes unir como has hccho antes
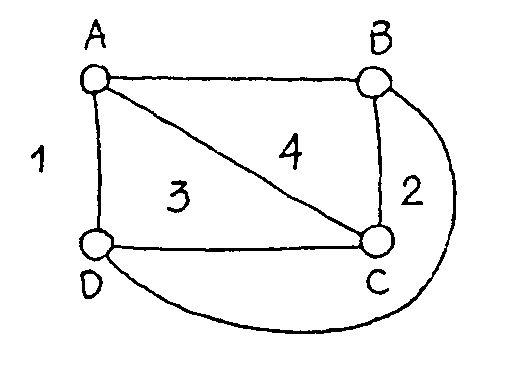
Ahora te preguntas: de entre las regiones del plano que
han resultado, ¿dónde podría quedar el quinto punto
E de modo que el problema fuese posible? Si está en 1 no se puede
unir a C, si está en 2 no se puede unir a A, si está en 3
no se puede unir a B y si está en 4 no se puede unir a D. Así
esté donde esté resulta que la tarea es imposible.
Otra tarea
imposible que alguna vez te habrán propuesto es la siguiente
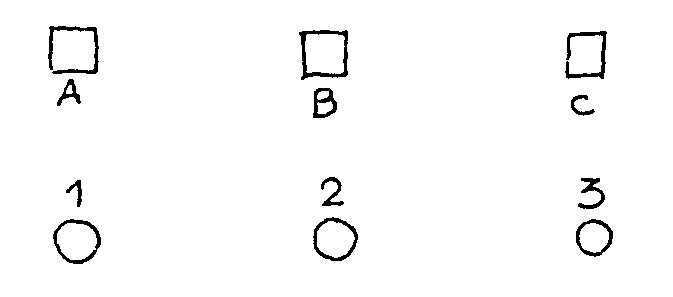
A, B, C son
tres granjas y 1,2,3 son tres pozos. Cada uno de los granjeros de A, B,
C quiere hacer tres conducciones de agua a cada uno de los tres pozos,
pero no quiere que su toma de agua se cruce con ninguna de las de los otros.
Es decir, se trata de trazar nueve líneas en el plazo A1, A2, A3,
B1, B2, B3, C1, C2, C3, que no se crucen. Inténtalo un rato pero
no demasiado largo. ¡El problema es imposible! Sin embargo, si los
granjeros vivieran en la cinta mágica que vamos a construir ahora,
el problema se les resolvería fácilmente.
Coge una tira
de papel así
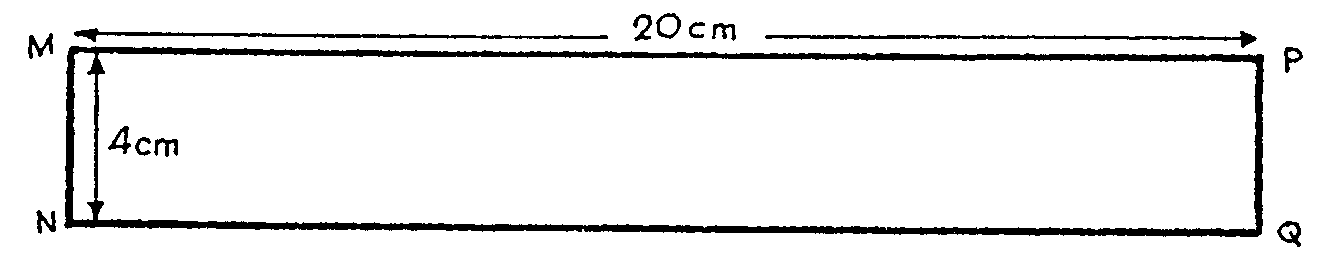
Vas a plegar sus bordes MN con PQ, pero antes de hacerlo
le das media vuelta al de la derecha. Así

A continuación los pegas de modo que Q vaya a
M y P a N. Te queda algo como esto que te pinto
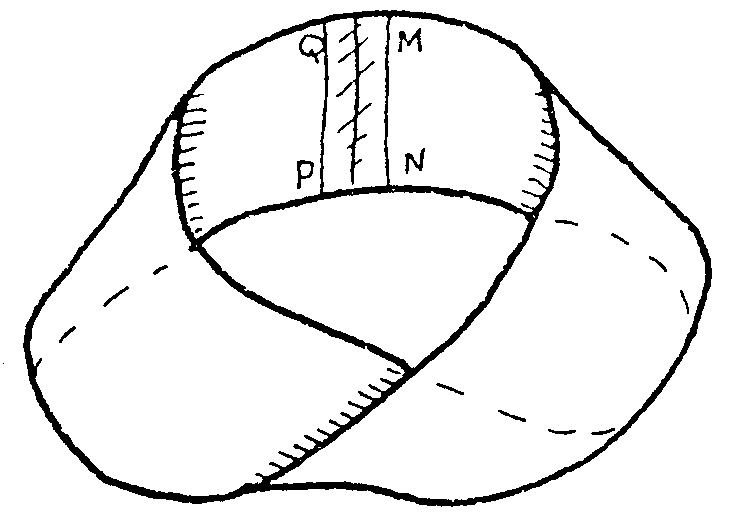
¡Ahí tienes la cinta de Möbius! ¿Qué
tiene de mágico? Coloca tus granjas y tus pozos. Así
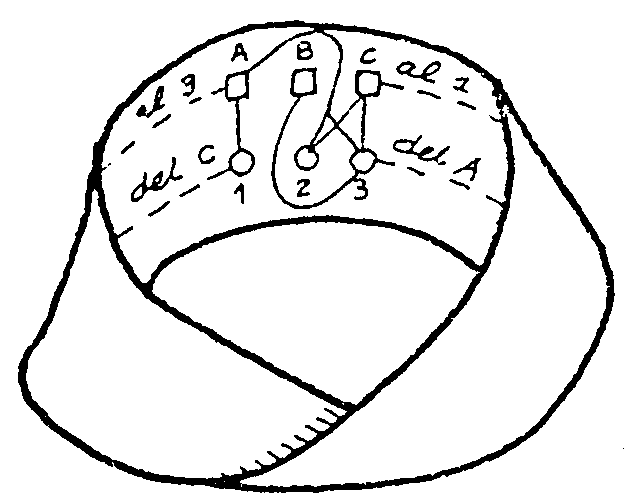
Trata de resolver ahora el problema de los granjeros
caprichosos. Desde A sales por una linea a la misma distancia del borde
que A y verás que llegas al punto 3... ¡sólo que por
detrás! Así mismo, saliendo de C por una línea a la
misma distancia del borde que C verás que llegas al punto 1... ¡también
por detrás!
Completar
las otras conducciones es cosa fácil.
También
el problema de los cinco puntos se resuelve de modo parecido sobre la cinta
de Möbius.
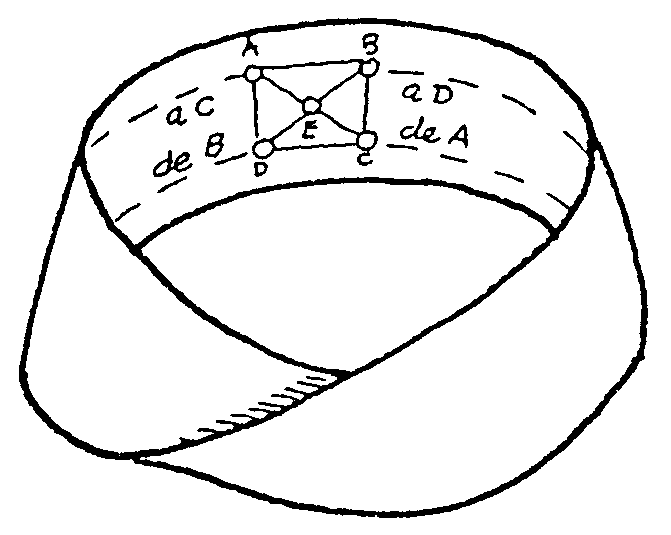
¿Se podrá resolver el problema semejante
de los seis puntos sobre la cinta de Möbius? ¡Si! ¡Ánimo!
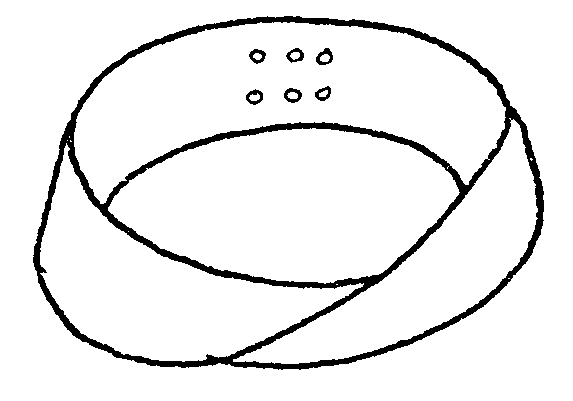
Parece que podemos decir: "Alto, Möbius! Has hecho trampa. Hemos llegado
a los puntos que queríamos, pero por el otro lado.
Así... ¡cualquiera lo hace!" "¿Otro
lado? ¿Qué otro lado?" diría Möbius-. "Si ves
dos lados en mi cinta, por favor píntame uno de azul y el otro de
negro". Trata de hacerlo con tus lápices. Empieza a pintar de negro
por algún sitio, sin pasar en ningún momento por ningún
borde, sigue, sigue... ¿Qué pasa? ¡Has pintado toda
la cinta! ¡No queda nada para pintar de azul! Y eso que no te has
pasado por ningún borde... La cinta tiene sólo lado. Es totalmente
distinta de una cinta cilíndrica. Hazte una así
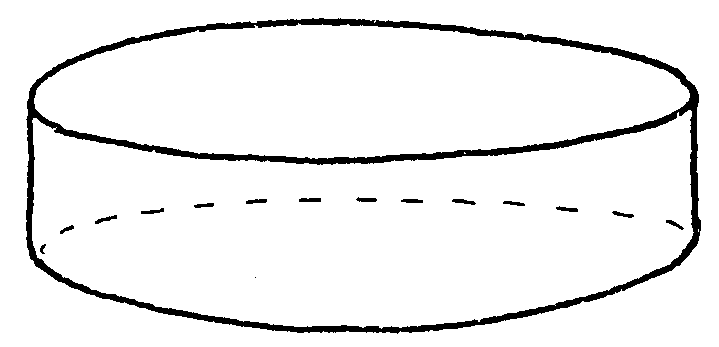
Aquí si empiezas a pintar de negro y no pasas
en ningún momento por el borde terminas pintando una cara y queda
otra para el azul. También se diferencia en otra cosa curiosa. La
cinta cilíndrica tiene claramente dos bordes. ¿Y la de Möbius?
Ve recorriendo el borde y comprobarás que de una pasada lo recorres
todo. La cinta de Möbius tiene sólo un borde y una sola cara.
La cinta de
Möbius presenta otras muchas sorpresas. En la cinta cilíndrica
de arriba metes unas tijeras y comienzas a cortar por una línea
paralela a los bordes

acabas llegando al punto de partida y salen dos cintas
cilíndricas parecidas a la primera separadas... ¡naturalmente!
Haz los mismo
con la cinta de Möbius. ¿Qué sale?...
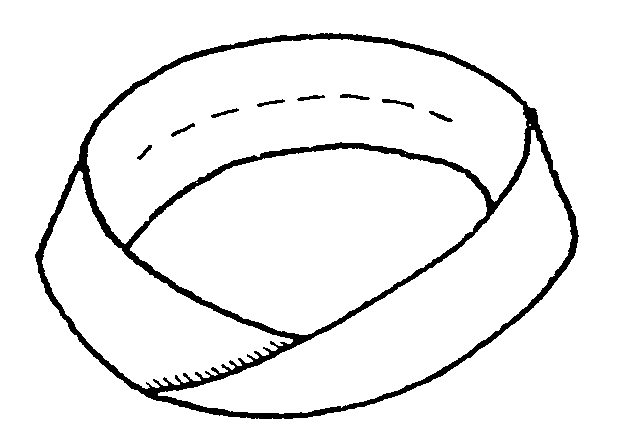
Curioso ¿no? Llegas al punto de partida y resulta
una sola cinta parecida a la que tenías, sólo que más
larga. ¿Será igual? Córtala otra vez por la mitad
a lo largo de una línea paralela al borde. Si fuera igual que la
primera le tendría que pasar lo mismo, es decir, tendría
que resultar otra cinta más larga ¿no? ¿Qué
sale? ¡Dos cintas enlazadas! Luego, no era igual. Hazte otra cinta
de Möbius y repite el experimento de dividirla por una línea
paralela al borde. Si te fijas bien en la cinta que te resulta observarás
fácilmente que tiene dos bordes y dos caras. Es como una cinta de
Möbius pero construída con dos medias vueltas en lugar de una.
Otro experimento
interesante. Corta una cinta de Möbius paralelamente a su borde comenzando
ahora a una distancia que sea más o menos un tercio de su anchura.
Así
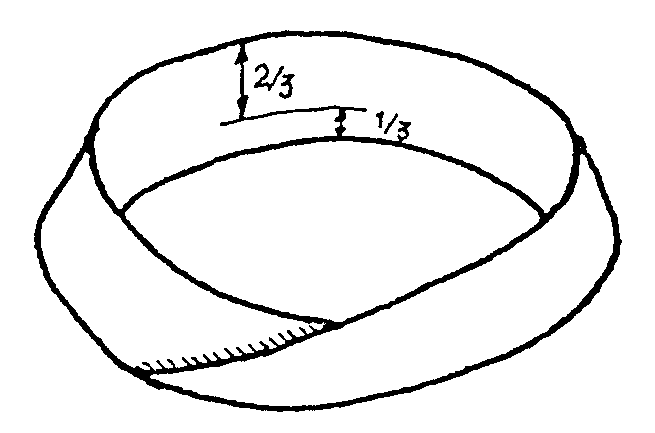
Verás que salen dos cintas enlazadas, una pequeña,
que es una cinta de Möbius de las de media vuelta, y otra más
grande con cuatro medias vueltas.
Ahora puedes
experimentar más por tu cuenta. Por ejemplo, puedes hacerte con
una cinta con cinco medias vueltas. ¿Cuántas caras tendrá?
¿Cuantos bordes? ¿Qué pasará si cortas por
la mitad? ¿Por qué no te haces con un procedimiento de adivinar
lo que va a pasar antes de hacerlo? Después de unas cuantas experiencias
seguro que das con la clave.