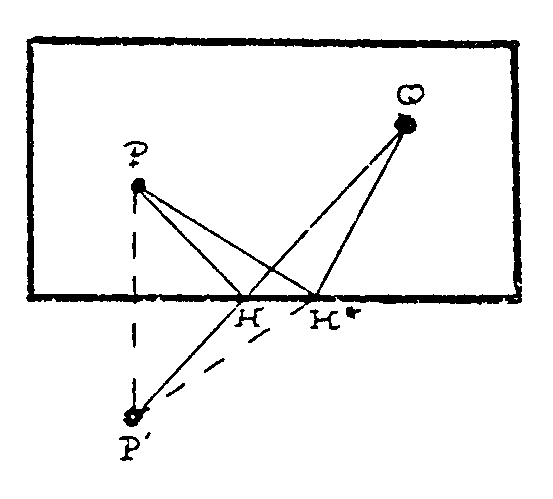VAMOS A JUGAR AL BILLAR  
 
        Tienes en el billar rectangular ABCD dos bolas en los puntos P y Q.
   
Quisieras tirar P contra la banda DC de modo que rebote hacia Q. ¿A qué punto de DC debes apuntar? Jugamos sin efectos. Así, si tiras desde P hacia un punto cualquiera H, la bola rebota en H formando con la banda el mismo ángulo con el que llegó. Un truco ingenioso para no tener que andar trazando ángulos iguales para cada vez que quieras saber hacia dónde va a salir rebotada la bola consiste en fijarte en que en todos los casos la dirección de salida pasa por el punto P´, simétrico de P respecto de la banda CD. Así, trazas P´ y de una vez para todas sabes por dónde sale la bola.
   
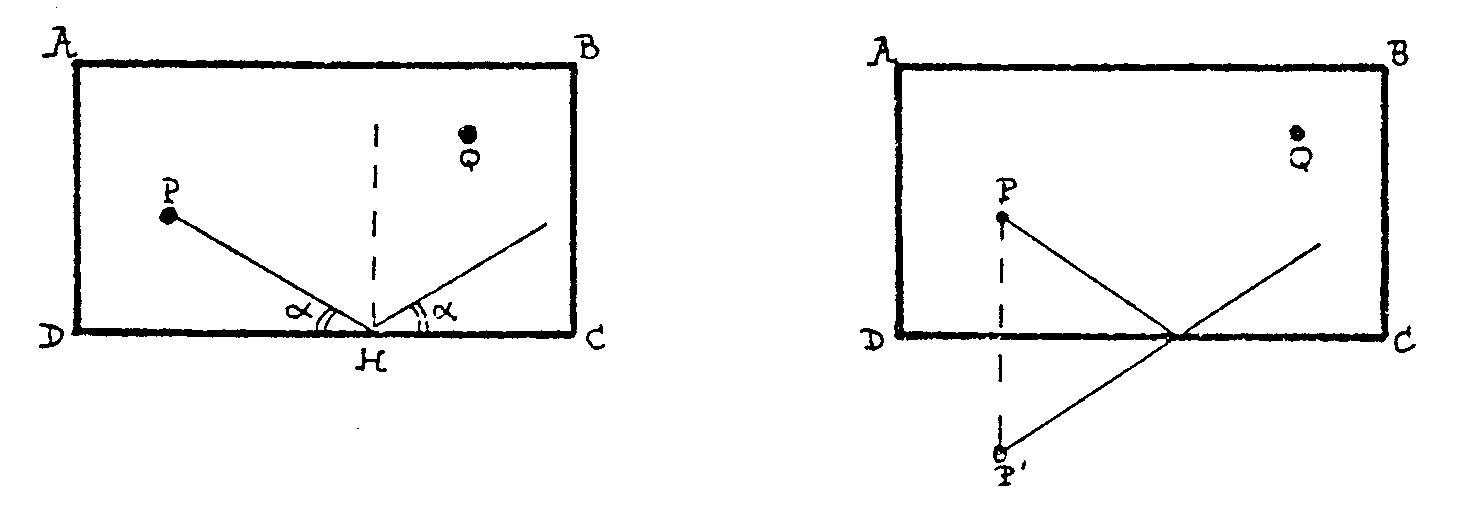
Basta unir P´ al punto de la banda al que apuntas y te puedes olvidar de trazar ángulos iguales. Observa que serán automáticamente iguales los ángulos que deben serlo ya que CD es mediatriz de PP´. Tu problema era mandar P a la banda CD de tal modo que se fuera rebotando hacia Q. Así es claro que te basta unir Q con P´ y ya tienes determinado el punto H al que has de enviar la bola.
   
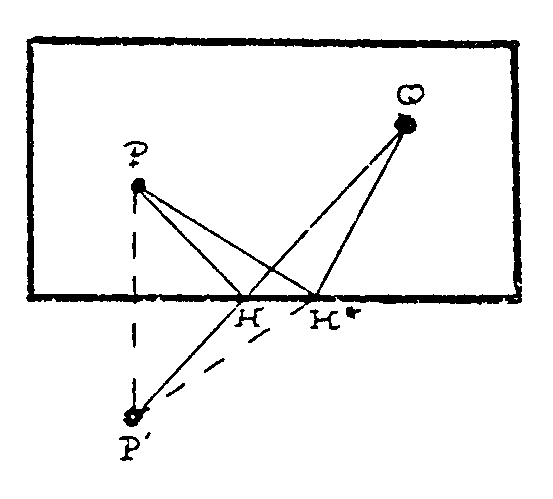
        Observa, pues será interesante más adelante, que el punto H es el punto de la banda DC que hace mínima la suma de segmentos PH+HQ. Fíjate que si tomas otro punto H* sobre la banda, entonces
 
H*P + H*Q = H*P´ + H*Q < P´Q = HP + HQ
 
siendo la desigualdad cierta, ya que la suma de dos lados en un triángulo es siempre mayor que el tercer lado.
 
        ¿Y si quisieras mandar P hacia Q después de rebotar primero en CD y luego en BC?
 
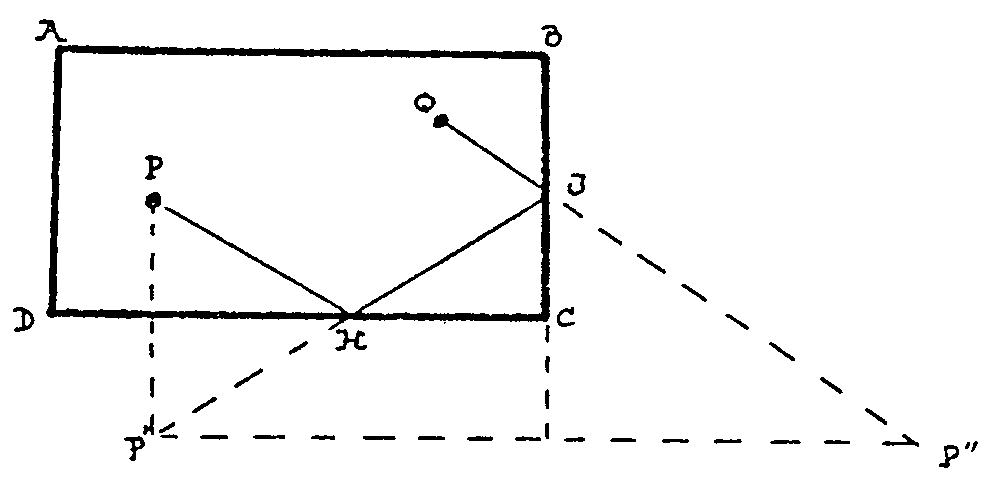
        Fíjate bien. Ya sabemos que al disparar la bola desde P hacia CD sale de la banda como si viniera de P´. Así, por las mismas cuentas, al rebotar ahora en la banda BC saldrá como si viniera de P´´, simétrico de P´ respecto de la banda BC. Si queremos que vaya a parar, después de este segundo rebote, al punto Q, no tenemos más que unir Q a P´´ y así obtenemos QJ, la última parte de la trayectoria de la bola. Como se trata de que llegue a J después de rebotar en DC, unimos J a P´ y obtenemos otro trozo HJ de la trayectoria. Finalmente unimos P con H y obtenemos la trayectoria que resuelve el problema propuesto.
   
        Naturalmente que a veces este último problema no tiene solución. Si al unir Q con P´´ resulta que el punto J se nos sale del billar, entonces no hay forma.
   
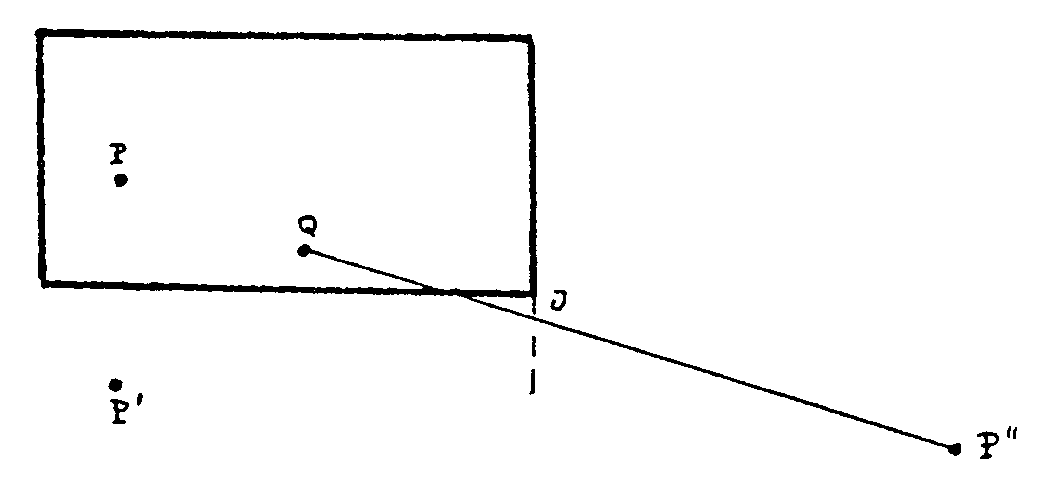
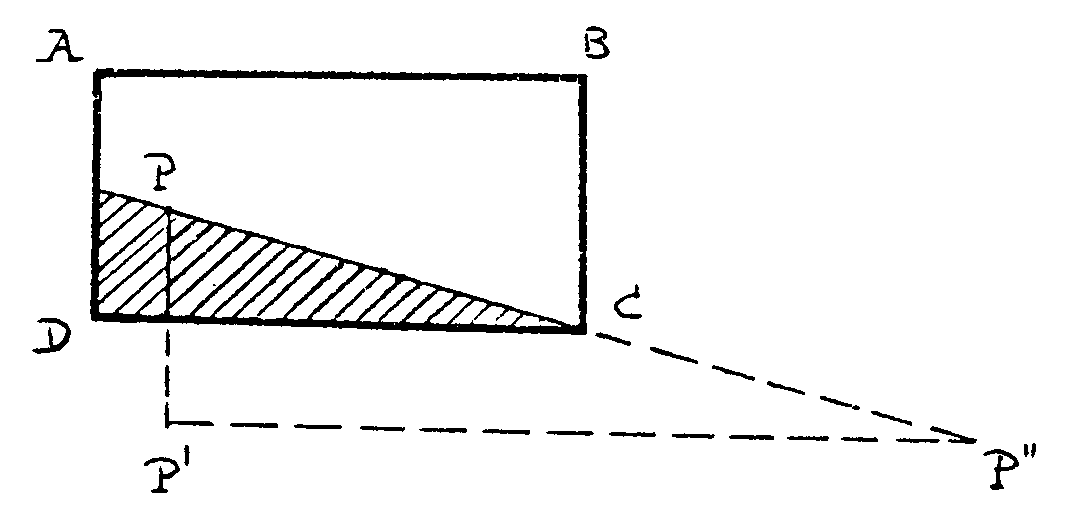
Así es claro que este problema, para un P fijo, tiene solución cuando Q está dentro de la zona no rayada de la figura siguiente.