UNA CURVA POLIVALENTE
En la cubierta
de la rueda de tu bici señala con tiza un punto que se vea bien
de lado. ¿Qué curva recorre ese punto cuando te mueves con
la bici por la carretera? Puedes tratar de pintar esa curva en tu papel.
No es difícil. Yo me he recortado un círculo de cartón
de unos 3,5 cm. de diámetro. Como es difícil conseguir que
ruede sin resbalar sobre mi regla, he sujetado al borde de mi regla un
trozo de papel celo con el lado engomado hacia afuera. He colocado la regla
sobre el papel y ahora sí que puedo hacer que la rueda ruede appoyada
en la regla y tumbada sobre el papel. En el borde de la rueda de cartón
he hecho una pequeña muesca para meter el lápiz. Con el lápiz
metido he hecho rodar el círculo a lo largo del borde de la regla
y mi lápiz me ha pintado esto
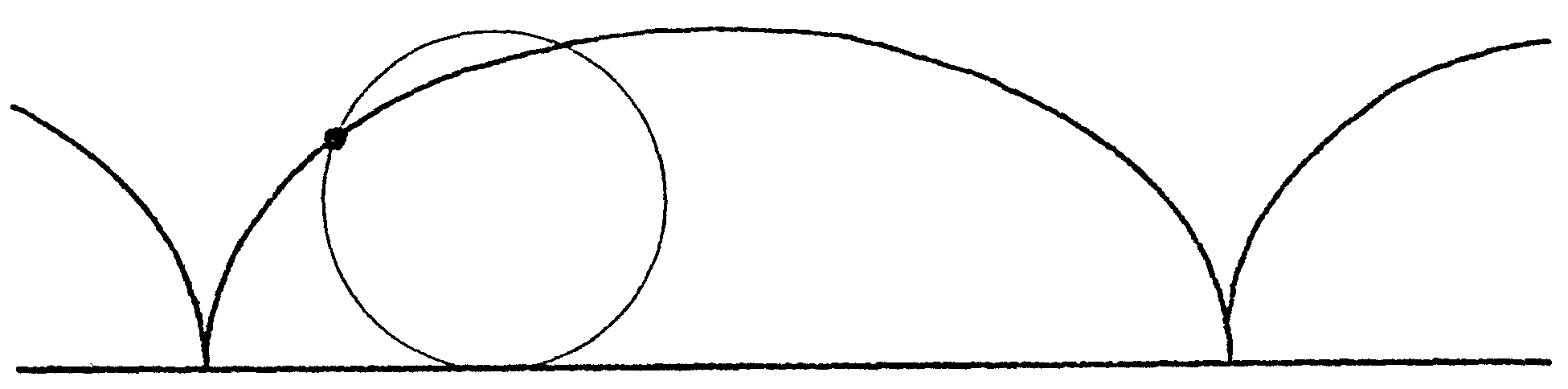
que da una buena idea de la curva. Esta curva es una
de las más famosas en la historia de las matemáticas. Se
llama la cicloide y tiene, como verás, un montón enorme de
propiedades curiosas.
Para empezar,
mira el área que queda entre un arco de cicloide y la recta sobre
la que ha rodado el círculo. ¿Qué área calculas
así a ojo que puede tener la superficie? Dirás, muy bien
dicho -¿Qué área... comparada con qué?- Parece
que tendrá algo que ver con la del círculo ¿no? Aquí
tienes las dos áreas
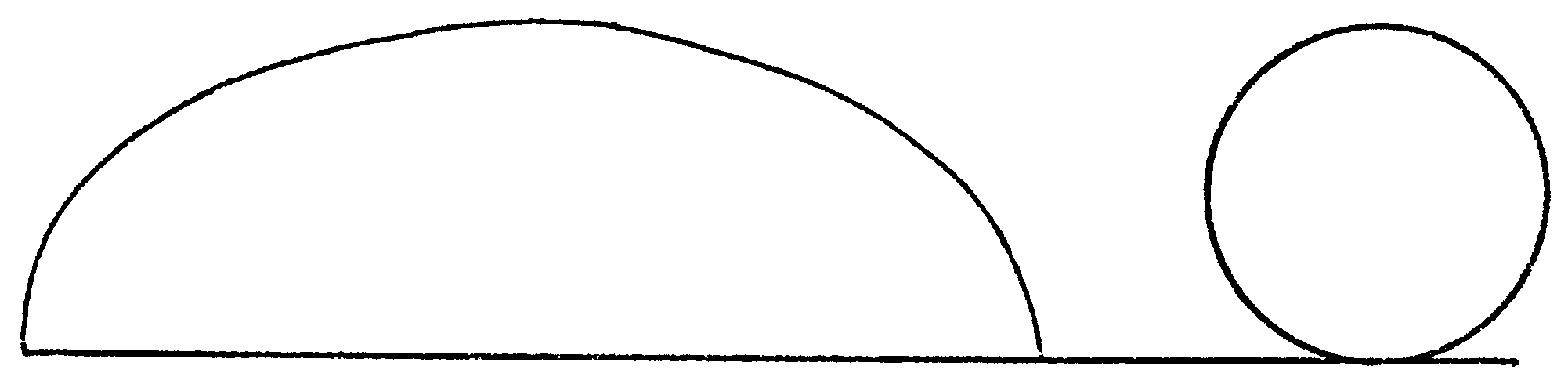
¿Cómo se te ocurre compararlas? Si tienes
papel milimetrado será fácil. Pintas sobre el papel milimetrado
las figuras, cuentas cuadraditos y comparas. Fácil... pero un poco
rollo eso de contar milímetros cuadrados. Galileo se interesó
por el problema. No tenía papel milimetrado, pero tenía una
balanza. Recortó las figuras sobre madera, las pesó y...
¡encontró que el área bajo la cicloide era como tres
veces el área del círculo! Pero le debió de parecer
que su método era inexacto y que la relación entre estas
áreas no podía ser 3, un número tan redondo, que no
tiene casi nada que ver con el número P,
sólo que está cerca de 3,141... Así que conjeturó
que el área bajo la cicloide tenía que ser P
veces la del círculo.
¡Se
debió de llevar una gran sorpresa cuando un francés, Roverbal
y un italiano discípulo suyo, Torricelli, llegaron a demostrar que
el área bajo la cicloide es exactamente tres veces el área
del círculo que da lugar a ella!.
Más
llamativo todavía resultó el cálculo de la longitud
de un arco de cicloide. ¿Por qué no tratas de averiguarlo
experimentalmente? Eso sí que es fácil. Recórtate
una cicloide en cartón grueso, coge un hijo y ponlo bordeando ese
cartón. ¡Y mide!. En mi cicloide, engendrada por mi rueda
de 3,5 cm. de diámetro, me sale que la longitud del hilo es de 14
cm. Prueba tú con otro tamaño, por ejemplo de 4 cm de diámetro.
¿Qué te sale? Más o menos 16 cm ¿qué
observas? 14/3,5 = 16/4 = 4. ¿Será verdad que la longitud
de la cicloide es 4 veces la del diámetro? ¡Sí! Y esto
es otro resultado de Roberval, Torricelli y otros hace unos tres
siglos.
Tal montón
de propiedades curiosas tiene la cicloide que aquellos señores del
siglo XVII comenzaron a estudiarla con fruición... y a organizar
unas terribles peleas sobre quién había encontrado primero
tal o cual propiedad. La siguiente se debe a Huygens, un holandés
nada errante que tenía su casa permanente en Groningen.
Recorta en
cartón dos medias cicloides como indica la figura
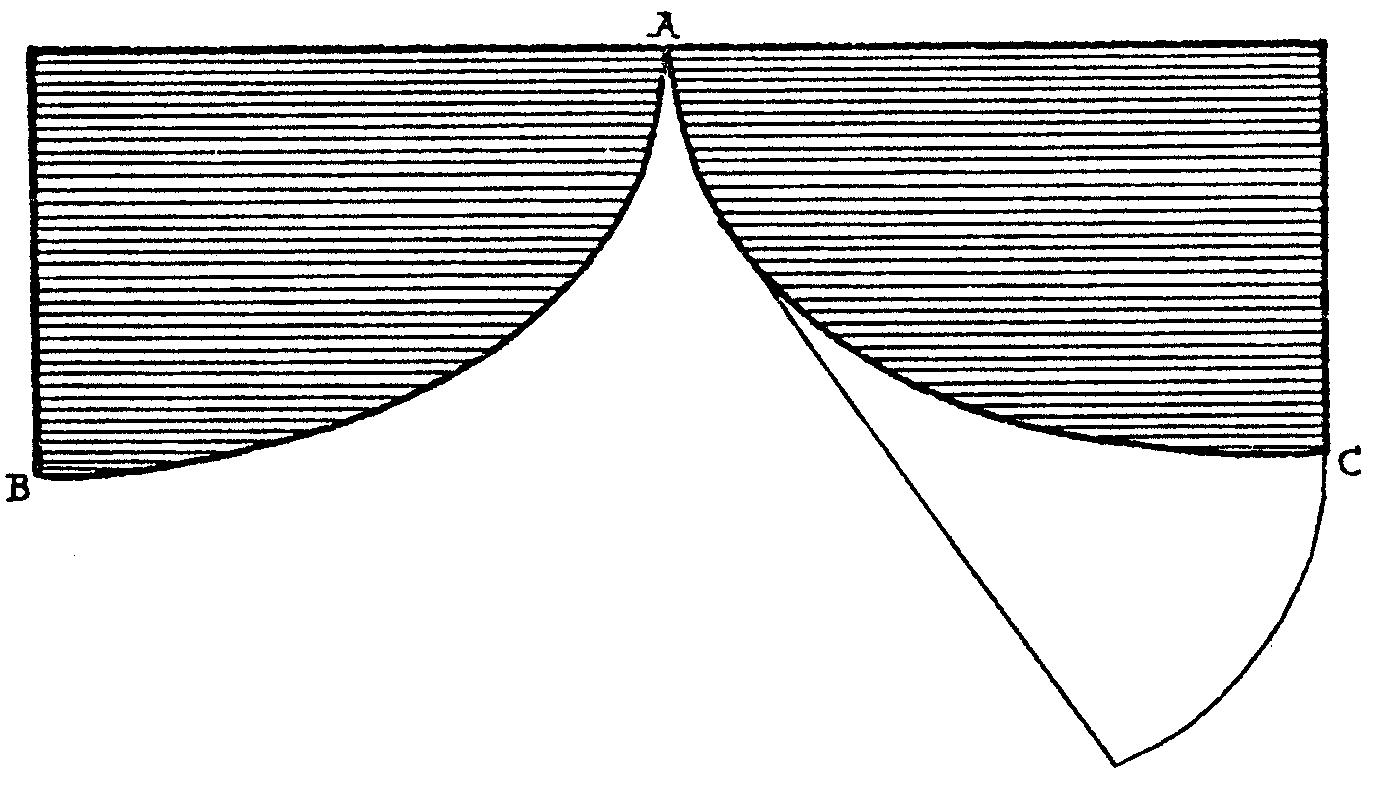
Coloca un hilo ajustado a la parte C y fija un estremo
en A. Sujeta la parte de tu lápiz al otro extremo en C y ahora,
con el extremo en A fijo y el hijo tenso, apoyado en el cartón,
sepáralo de C dejándolo describir una curva. ¿Qué
curva? Hazlo primero y adivina después. ¡Sí! Es una
cicloide igual a las de arriba, sólo que entera, como indica el
dibujo.
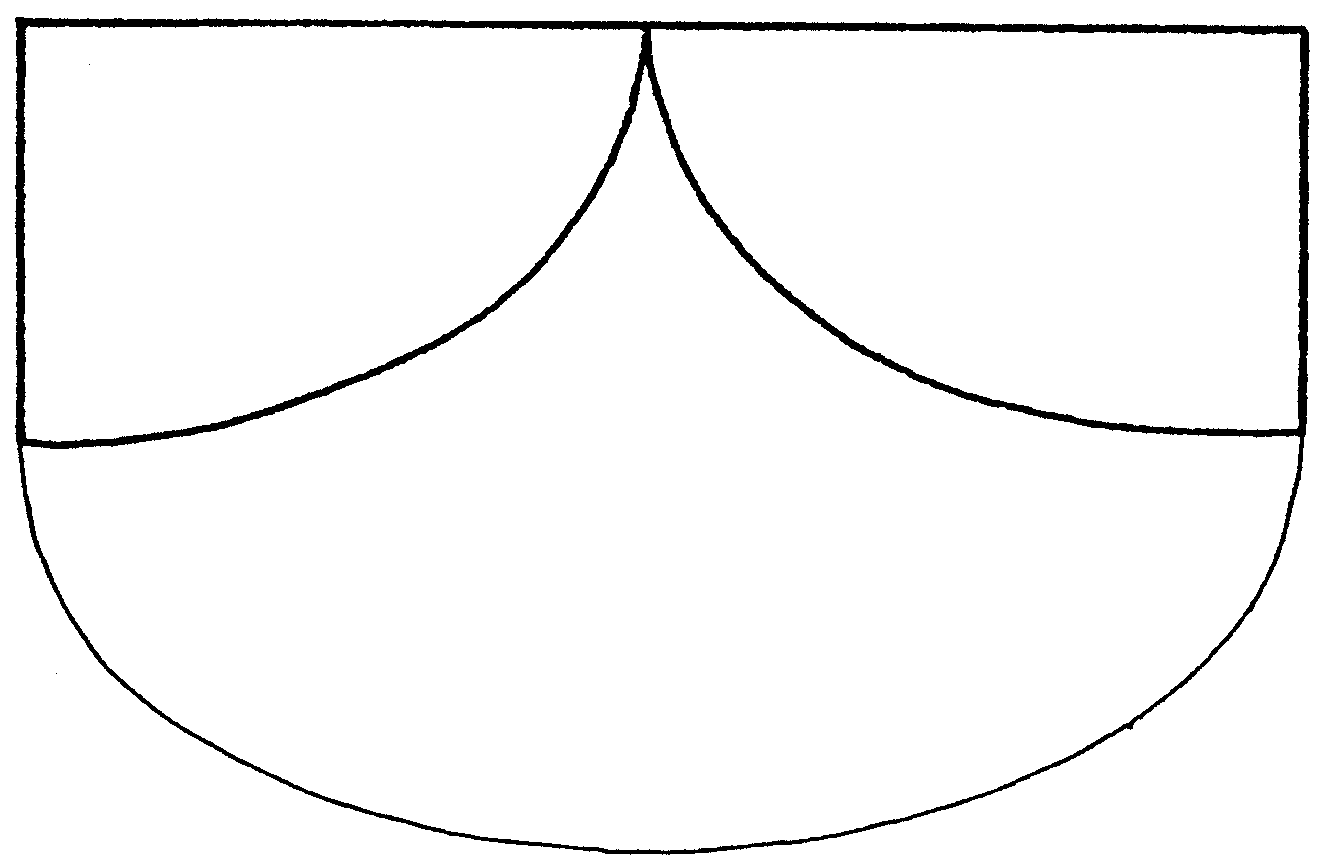
Huygens fue
el primer constructor serio de relojes de péndulo, a la vez que
un matemático y físico genial del siglo XVII. Se hizo un
péndulo así
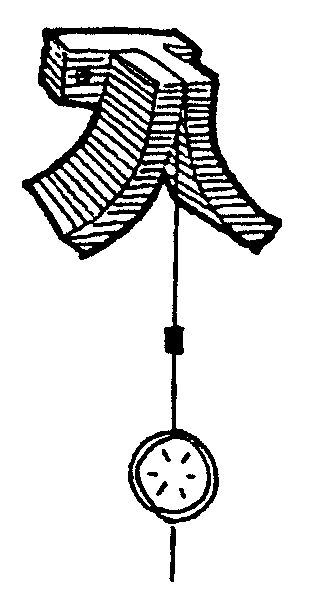 que tenía la siguiente propiedad muy especial: aun
cuando la amplitud del movimiento del péndulo varíe y se
haga más grande o más pequeña, el péndulo sigue
marcando el tiempo igualmente bien, es decir, tiene el mismo período.
que tenía la siguiente propiedad muy especial: aun
cuando la amplitud del movimiento del péndulo varíe y se
haga más grande o más pequeña, el péndulo sigue
marcando el tiempo igualmente bien, es decir, tiene el mismo período.
¿A
qué se debe esto? Huygens descubrió que la cicloide tiene
la propiedad de ser nada menos que tautócrona. ¿Qué
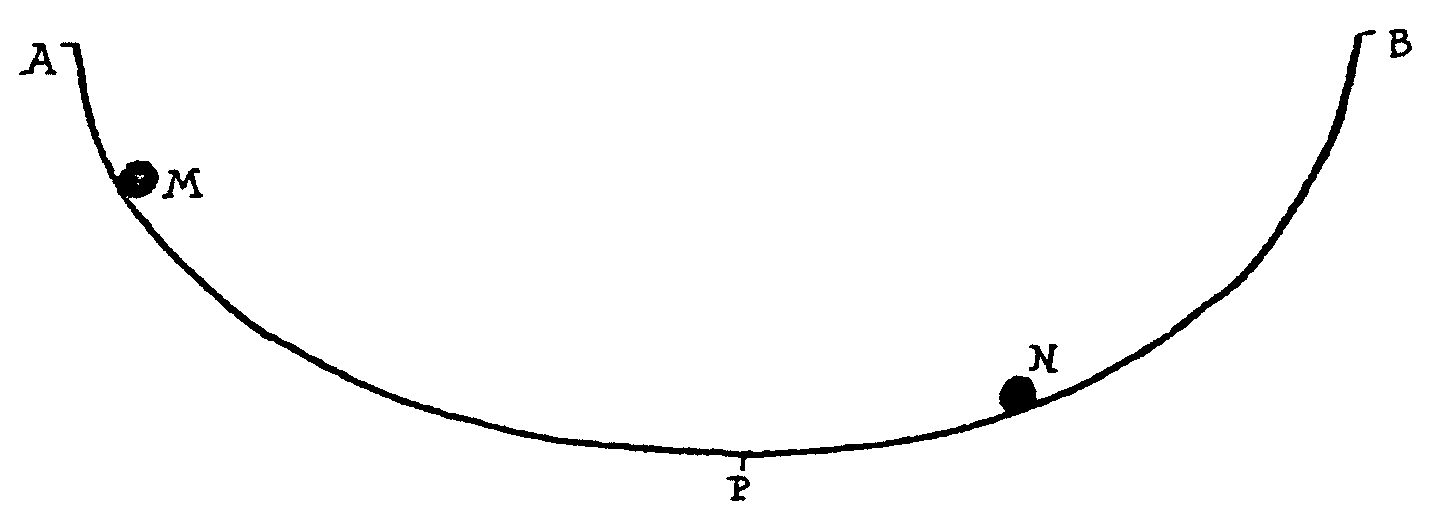
qué es eso? Pues eso consiste en lo siguiente: si colocas una cicloide
hacia arriba, como en el dibujo siguiente y dejas caer dos canicas por
ella, una desde el punto M y otra desde el N, ... ¡las dos
llegan al punto P más bajo de la cicloide al mismo tiempo!
Y eso que la que baja desde M tiene que recorrer un camino mayor.
Esta propiedad te explica que si te puedes construir
un péndulo tal que la lenteja recorra, no un arco de círculo,
como en los relojes de péndulo que vemos hoy día, sino un
arco de cicloide, entonces no importa que la amplitud sea mayor o menor.
Su período es el mismo. Huygens se las ingenió, con la propiedad
que hemos visto antes, para que la lenteja recorriera, efectivamente, una
cicloide. Observa en el dibujo del péndulo de Huygens que los dos
topes de la cuerda son dos arcos de cicloide.
Para experimentar
esto de la tautocronía de la cicloide yo me he hecho un experimento
bastante sencillo. ¿Por qué no me sigues y te lo haces tú
mismo? Recorta un cartón de modo que el borde sea una cicloide bien
grande, cuanto más grande mejor. Córtalo por la mitad, por
la línea de puntos del dibujo.
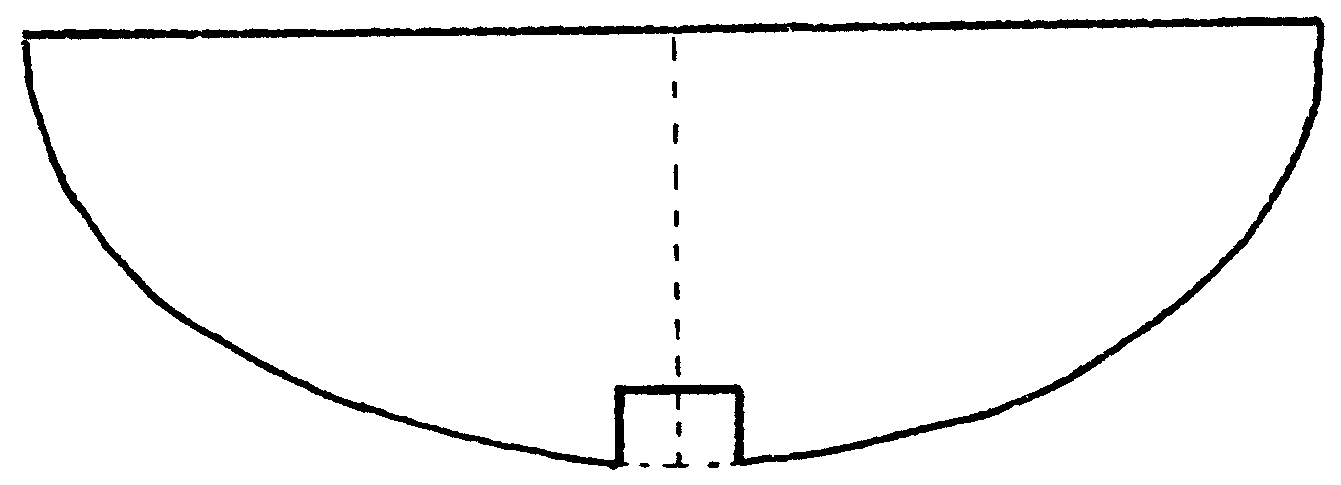
Recorta también
dos trocitos por el borde de abajo de modo que quepa a través de
cada uno de los agujeros una canica.
Pega un trozo
de cartulina por el borde de cada mitad de modo que quede algo así
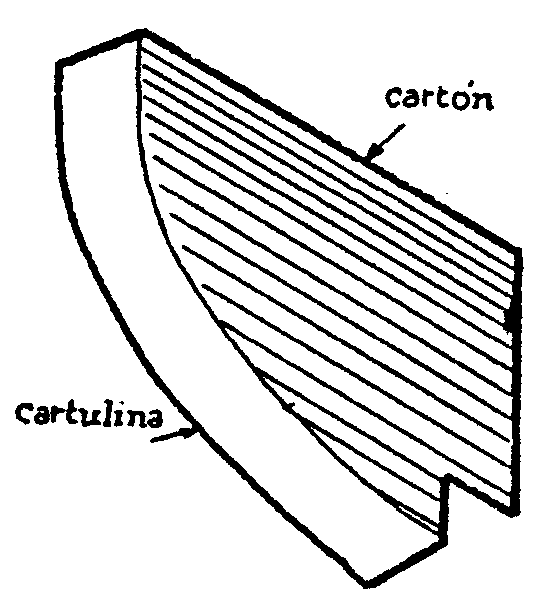
Procura que el borde exterior de la cartulina quede un
poco levantado para que una canica pueda bajar por ella sin salirse, siguiendo
la línea de la cicloide.
Ahora, con
un papel de celo une los dos trozos de cicloide que has preparado en ángulo
recto. Te debe quedar algo así
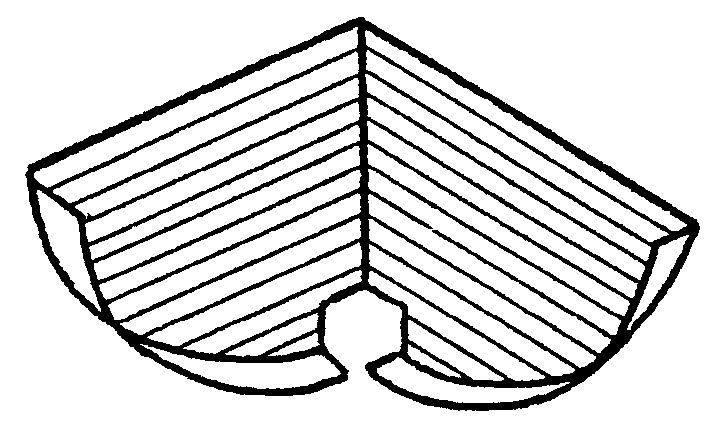
Ahora ya puedes empezar a experimentar. Vas a necesitar
cuatro manos, de modo que ya puedes ir llamando a algún amigo. Tu
amigo te sostiene el chisme que has preparado verticalmente. Tú
dejas caer al tiempo dos canicas, una por cada mitad de la cicloide
desde puntos de la cicloide situados a diferentes alturas. Si las
cosas las has hecho bien, las dos canicas se chocarán en el punto
más bajo, puesto que llegan allí al mismo tiempo.
Si es que salen mal las cosas, una llegará antes que la otra y las
dos se saldrán por los agujeros a toda velocidad.
A la cicloide
no le basta con ser tautócrona, porque además es braquistócrona,
ya que es ser...¿no? Ser braquistócrona significa
ser la curva de descenso más rápido, en el siguiente sentido.
Señala dos puntos A y B en un plano vertical, a distinta altura.

Suponte que tienes un alambre y una cuenta de rosario.
Se trata de unir A y B con el alambre, de ensartar la cuenta en A y de
hacerla caer por el alambre hasta B. Para cada forma de curva que le des
al alambre la cuenta tardará un tiempo distinto en caer de A a B.
La pregunta es ahora: ¿qué forma habrá que darle al
alambre para que la cuenta llegue a B en el menor tiempo posible? ¡Pues
resulta que la forma es precisamente la de la cicloide que sale verticalmente
de A y pasa por B, del siguiente modo
Curioso ¿no? El segmento rectilíneo AB
da la distancia menor entre A y B pero una bola que cae por el plano indicado
AB... ¡Tarda más por ahí que si va por APB, bajando
primero hasta P y luego subiendo a B! ¡Quién lo diría!
¿Por
qué no te haces el experimento, como antes, con cartón y
cartulinas y canicas? ¡Es fácil! Si tu cicloide es bien grande
podrás observar la diferencia.













