radianes.
En este caso tenemos un triángulo equilátero por lo que las espirales
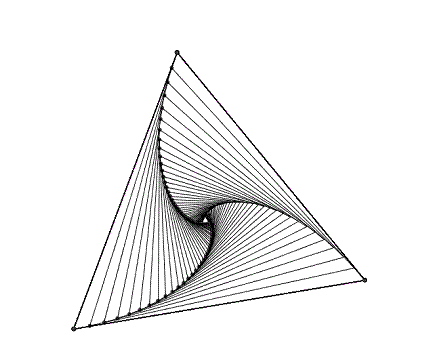
equiangulares serán de π/6 radianes.Modelo 3 insectos
Hemos explicado que si tenemos
un polígono regular de n caras el rastro que dejan los insectos son espirales
equiangulares de radianes.
En este caso tenemos un triángulo equilátero por lo que las espirales
equiangulares serán de π/6 radianes.
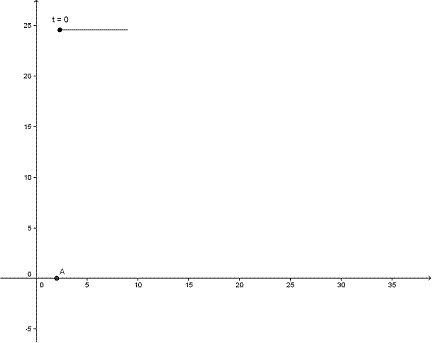
El primer paso que debemos hacer es crear un deslizador t para construir nuestras curvas. Le pondremos un intervalo con extremo inferior 0. Tenemos que tener en cuenta que los tres insectos se encontrarán en el centro del triángulo, que constituirá el punto inicial de las tres espirales por lo que podemos construirlas de tal forma que para t=0 las tres coincidan en el centro.
Empecemos por el primer insecto, situado en el punto A. Tendrá de ecuaciones:
A= (-1 e^(t / tan(π / 6)) cos(t) + 3, e^(t / tan(π / 6)) sin(t)).
Lo podemos colocar en el punto que queramos. En este caso hemos seleccionado el punto (2,0) (a ello se debe el 3 en las ecuaciones) como el centro del triángulo, es decir, el punto final de la trayectoria que describe el insecto ya que éste recorrerá la espiral de fuera hacia adentro.
A continuación situaremos el punto B. La trayectoria que seguirá este insecto será la misma espiral equiangular del insecto en A, ya que ambos poseen la misma velocidad, pero deberemos rotarla 2 π/3. Éste es el ángulo formado por los segmentos que unen el centro con dos de los vértices del triángulo equilátero.
En principio, B= (-1 e^(t / tan(π / 6)) cos(t + 2 π / 3) + 3, e^(t / tan(π / 6)) sin(t + 2 π / 3)), pero pronto nos damos cuenta de que para t=0 no coincide con el punto A, por lo que deberemos ajustar su ecuación. Nos queda finalmente la siguiente ecuación:
B= (-1 e^(t / tan(π / 6)) cos(t + 2 π / 3) + 1.5, e^(t / tan(π / 6)) sin(t + 2 π / 3) - 0.87)
Realizamos el mismo proceso con C.
C= (-1 e^(t / tan(π / 6)) cos(t + 2 π / 3) + 1.5, e^(t / tan(π / 6)) sin(t + 2 π / 3) - 0.87)
*Recuerda que en Geogebra puedes activar el rastro que dejan los elementos. En nuestro modelo escoge la opción decremento en el apartado de animación. Puedes también variar el incremento del intervalo.
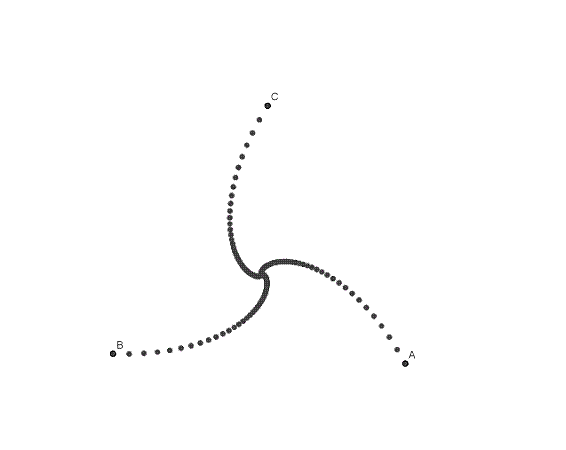
Si queremos mostrar las líneas de dirección de cada insecto construimos los segmentos AB, BC y CA.
Podemos apreciar que cada línea es tangente a los espirales y forma parte un polígono semejante al original, luego, la espiral formada debe ser una equiangular.
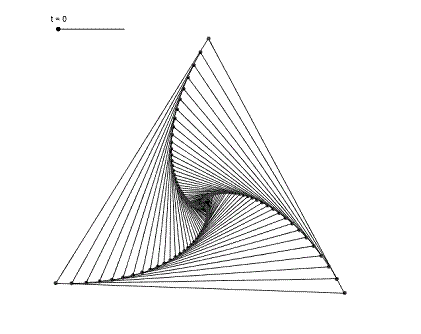
Podemos aumentar el valor del extremo inferior del deslizador para que no lleguen a encontrarse en nuestro dibujo y quede en blanco el centro del triángulo.
