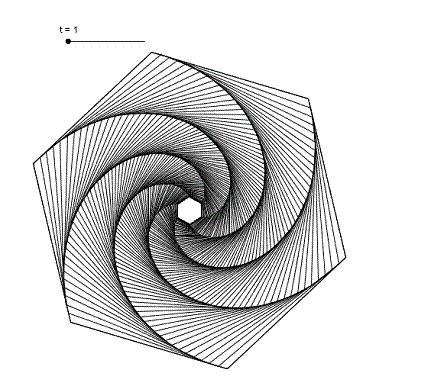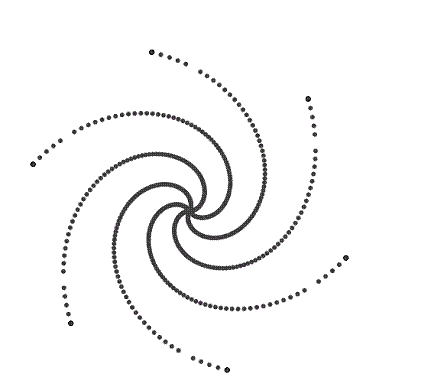
Modelo 6 insectos
En este caso tenemos un pentágono regular por lo que las espirales equiangulares serán de π/3 radianes.
El método para la construcción es idéntico al de los modelos anteriores por lo que sólo escribiremos las ecuaciones de las espirales.
A= (e^(t / tan(π / 3)) cos(t), e^(t / tan(π / 3)) sin(t))
A continuación situaremos el punto B. Deberemos rotarla espiral anterior π/3. Éste es el ángulo formado por los segmentos que unen el centro con dos vértices consecutivos del pentágono regular.
Después del ajuste nos queda la siguiente ecuación:
B= (e^(t / tan(π / 3)) cos(t + π / 3) + 0.5, e^(t / tan(π / 3)) sin(t + π / 3) - 0.87)
Realizamos el mismo proceso con C, D y E obteniendo:
C= (e^(t / tan(π / 3)) cos(t + 2 π / 3) + 1.5, e^(t / tan(π / 3)) sin(t + 2 π / 3) - 0.87)
D= (e^(t / tan(π / 3)) cos(t + π) + 2, e^(t / tan(π / 3)) sin(t + π))
E= (e^(t / tan(π / 3)) cos(t + 4 π / 3) + 1.5, e^(t / tan(π / 3)) sin(t + 4 π / 3) + 0.87)
F= (e^(t / tan(π / 3)) cos(t + 5 π / 3) + 0.5, e^(t / tan(π / 3)) sin(t + 5 π / 3) + 0.87)

Si queremos mostrar las líneas de dirección de cada insecto construimos los segmentos AB, BC, CD, DE, EF y FA.
Podemos apreciar que cada línea es tangente a los espirales y forma parte un polígono semejante al original, luego, la espiral formada debe ser una equiangular.

Podemos aumentar el valor del extremo inferior del deslizador para que no lleguen a encontrarse en nuestro dibujo y quede en blanco el centro del triángulo.