Full paper in PDF format:
$%G. Gromadzki, On conjugacy of p-gonal automorphisms of Riemann surfaces, Rev. Mat. Complut. 21 (2008), no. 1, 83–87.%$
On Conjugacy of p-gonal Automorphisms
of Riemann Surfaces
Grzegorz GROMADZKI
Received: January 8, 2007
Accepted: August 30, 2007
The classical Castelnuovo-Severi theorem implies that for 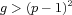 , a
, a
 -gonal automorphism group of a cyclic
-gonal automorphism group of a cyclic  -gonal Riemann surface
-gonal Riemann surface 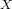 of
genus
of
genus  is unique. Here we deal with the case
is unique. Here we deal with the case  ; we give a new
and short proof of a result of González-Diez that a cyclic
; we give a new
and short proof of a result of González-Diez that a cyclic  -gonal Riemann
surface of such genus has one conjugacy class of
-gonal Riemann
surface of such genus has one conjugacy class of  -gonal automorphism groups
in the group of automorphisms of
-gonal automorphism groups
in the group of automorphisms of  .
.
Key words: automorphisms of Riemann surfaces, fixed points, ramified coverings of
Riemann surfaces, hyperellipticity.
2000 Mathematics Subject Classification: Primary 30F10; Secondary 14H37, 14H55.
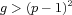 , a
, a
 -gonal automorphism group of a cyclic
-gonal automorphism group of a cyclic  -gonal Riemann surface
-gonal Riemann surface 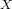 of
genus
of
genus  is unique. Here we deal with the case
is unique. Here we deal with the case 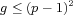 ; we give a new
and short proof of a result of González-Diez that a cyclic
; we give a new
and short proof of a result of González-Diez that a cyclic  -gonal Riemann
surface of such genus has one conjugacy class of
-gonal Riemann
surface of such genus has one conjugacy class of  -gonal automorphism groups
in the group of automorphisms of
-gonal automorphism groups
in the group of automorphisms of 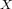 .
.