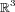will illustrate the theory. A forthcoming
work (Part II) will complete the present one by the study of the Steklov-Poincaré
operator related to this equation when the length 
of the interval tends to
zero.
Full paper in PDF format:
$%A. Favini, R. Labbas, K. Lemrabet, and B.-K. Sadallah, Study of a complete abstract
differential equation of elliptic type
with variable operator coefficients, I, Rev. Mat. Complut. 21 (2008), no. 1, 89–133.%$
|
|||
|
|||
ABSTRACT
The aim of this first work is the resolution of an abstract complete second order
differential equation of elliptic type with variable operator coefficients set in a
small length interval. We obtain existence, uniqueness and maximal regularity
results under some appropriate differentiability assumptions combining those of
"On the abstract evolution equation of parabolic type" (Yagi, 1977) and
"Sommes d'opérateurs linéaires et équations différentielles
opérationnelles" (Da Prato-Grisvard, 1975). An example for the
Laplacian in a regular domain of 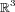will illustrate the theory. A forthcoming
work (Part II) will complete the present one by the study of the Steklov-Poincaré
operator related to this equation when the length of the interval tends to
zero.
Key words: abstract differential equations of second order, variable operator coefficients,
mixed boundary conditions, maximal regularity, compatibility conditions.
2000 Mathematics Subject Classification: 34G10, 34K10,34K30, 35J25, 44A45, 47D03.