Full paper in PDF format:
$%C. Schneider, On dilation operators in Besov spaces, Rev. Mat. Complut. 22 (2009), no. 1,
111–128.%$
On Dilation Operators in Besov Spaces
Cornelia SCHNEIDER
Received: April 22, 2008
Accepted: May 6, 2008
We consider dilation operators 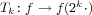 in the framework of Besov
spaces
in the framework of Besov
spaces 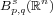 when
when 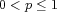 . If
. If 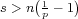 ,
, 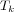 is a bounded
linear operator from
is a bounded
linear operator from 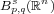 into itself and there are optimal bounds
for its norm. We study the situation on the line
into itself and there are optimal bounds
for its norm. We study the situation on the line 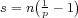 , an open
problem mentioned in "Function spaces, entropy numbers,
differential operators" (Edmunds and Triebel, 1996). It turns out that the results shed
new light upon the diversity of different approaches to Besov spaces on this
line, associated to definitions by differences, Fourier-analytical methods, and
subatomic decompositions.
, an open
problem mentioned in "Function spaces, entropy numbers,
differential operators" (Edmunds and Triebel, 1996). It turns out that the results shed
new light upon the diversity of different approaches to Besov spaces on this
line, associated to definitions by differences, Fourier-analytical methods, and
subatomic decompositions.
Key words: Besov spaces, dilation operators, moment conditions.
2000 Mathematics Subject Classification: 46E35.
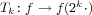 in the framework of Besov
spaces
in the framework of Besov
spaces 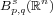 when
when 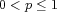 . If
. If 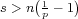 ,
, 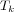 is a bounded
linear operator from
is a bounded
linear operator from 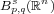 into itself and there are optimal bounds
for its norm. We study the situation on the line
into itself and there are optimal bounds
for its norm. We study the situation on the line 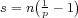 , an open
problem mentioned in "Function spaces, entropy numbers,
differential operators" (Edmunds and Triebel, 1996). It turns out that the results shed
new light upon the diversity of different approaches to Besov spaces on this
line, associated to definitions by differences, Fourier-analytical methods, and
subatomic decompositions.
, an open
problem mentioned in "Function spaces, entropy numbers,
differential operators" (Edmunds and Triebel, 1996). It turns out that the results shed
new light upon the diversity of different approaches to Besov spaces on this
line, associated to definitions by differences, Fourier-analytical methods, and
subatomic decompositions.