Full paper in PDF:
$%M. Yahdi, The topological complexity of sets of convex differentiable
functions,
Rev. Mat. Complut. 11 (1998), no. 1, 79–91.
%$
The Topological Complexity of Sets of
Convex Differentiable Functions
Mohammed YAHDI
Equipe d’Analyse
Université Paris VI
Boîte 186
4 Place Jussieu
75252 Paris Cedex 05 — France
Received: September 9, 1996
ABSTRACT
Let 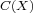 be the set of all convex and continuous functions on a separable
infinite dimensional Banach space
be the set of all convex and continuous functions on a separable
infinite dimensional Banach space 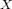 , equipped with the topology of uniform
convergence on bounded subsets of
, equipped with the topology of uniform
convergence on bounded subsets of 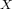 . We show that the subset of all convex
Fréchet-differentiable functions on
. We show that the subset of all convex
Fréchet-differentiable functions on 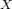 , and the subset of all (not necessarily
equivalent) Fréchet-differentiable norms on
, and the subset of all (not necessarily
equivalent) Fréchet-differentiable norms on 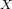 , reduce every coanalytic set, in
particular they are not Borel-sets.
, reduce every coanalytic set, in
particular they are not Borel-sets.
1991 Mathematics Subject Classification: 54H05, 46B20, 58C20.
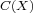 be the set of all convex and continuous functions on a separable
infinite dimensional Banach space
be the set of all convex and continuous functions on a separable
infinite dimensional Banach space 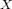 , equipped with the topology of uniform
convergence on bounded subsets of
, equipped with the topology of uniform
convergence on bounded subsets of 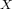 . We show that the subset of all convex
Fréchet-differentiable functions on
. We show that the subset of all convex
Fréchet-differentiable functions on 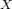 , and the subset of all (not necessarily
equivalent) Fréchet-differentiable norms on
, and the subset of all (not necessarily
equivalent) Fréchet-differentiable norms on 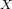 , reduce every coanalytic set, in
particular they are not Borel-sets.
, reduce every coanalytic set, in
particular they are not Borel-sets.