Experimenting with Morley's triangle.

A reminder:

Morley's theorem:

For an arbitrary triangle ABC one draws the trisector lines of angles at A, B, C. Then the two trisector lines at B and C which are closer to the side a intersect at point M. In an analogous way one determines points N and P.
Then the triangle MNP is  equilateral.
 

A set of DERIVE functions which give the Morley's triangle of a given triangle.

Experimenting with this beautiful theorem:

Sometimes strange phenomena happen with the experiments. It would seem then in every case this equilateral triangle should be in the interior of the initial triangle, but...


We experiment by rotating the same triangle
around one of its vertices


The reason?
The DERIVE function ATAN gives us values between -p/2 and p/2. For this reason the program was producing sometimes the trisector lines interior to the angles at A, B, C and some other times the trisector lines of the exterior angles.

To confirm this point one can make
an easy experiment with DERIVE.
Changing the function ATAN so that it gives us values between 0 and p we obtain the following 'Morley' triangles:

with new ATAN                              with old ATAN

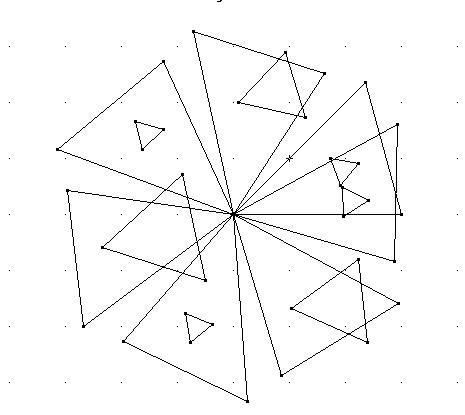
But... the triangles which result seem to keep being equilateral.

Perhaps a different new theorem behind?

For an angle a we consider
the two external trisector lines as follows:
Then in Morley's theorem:

One can choose the  trisector lines for the three  external angles.
The resulting triangle is equilateral.











Yes... a different theorem, but not new:

W.R. Spickerman, An extension of Morley's theorem, Math. Magazine 44 (1971) 191-192.
 

But according to our experiments...

One can also choose the trisector lines for two internal angles and the  ones for the other external third angle.
The resulting triangle is equilateral. The proof can follow the same pattern as in the other cases.
One also can observe that all the 5 equilateral 'Morley' triangles have sides which are parallel, i.e. there are just three directions for all the sides. It is easy to measure the inclination over the sides of the original triangle.

(New?) Anyway the bright idea belongs to Morley.

But this is not true when one takes the trisector lines of two external angles and the trisector lines of the interior of the third one.

Are there still more 'Morley' triangles?
Are there still more beautiful properties?
An invitation to explore further...