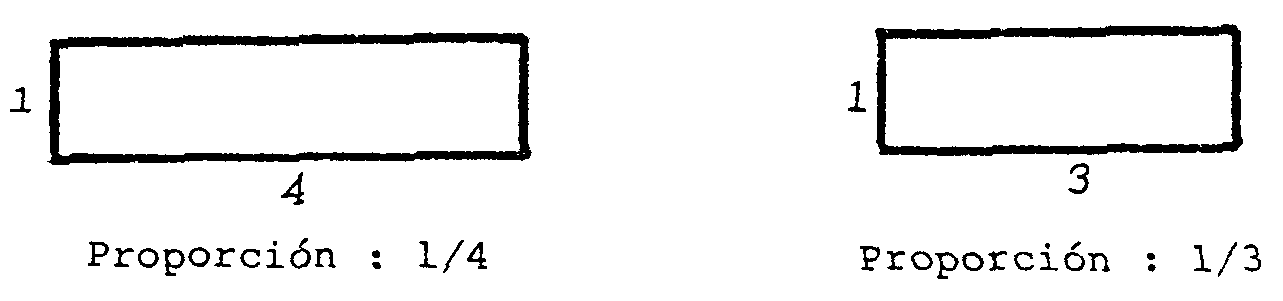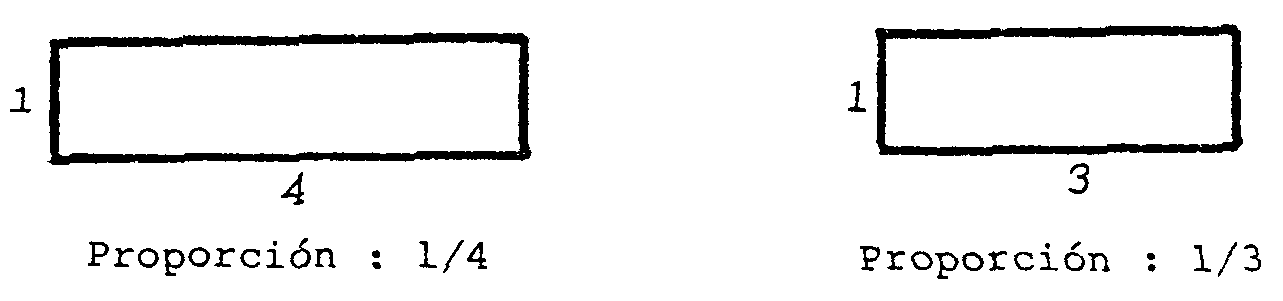EN BUSCA DEL MEJOR FOLIO             El rectángulo y el cuadrado tienen bastantes cosas en común, pero al mismo tiempo tienen otras que los distinguen bien claramente. Si dices a un amigo: -"Dibújame un rectángulo"- y te contesta: -"¿Lo quieres grande o pequeño, gordo o delgado?"-, no te extrañas. Pero si le dices: -"Dibújame un cuadrado"- y te contesta: -"¿Lo quieres gordo o delgado?"-, entonces pensarás que no ha entendido bien lo que es un cuadrado. Los cuadrados pueden ser grandes o pequeños, pero no pueden ser más delgados o más gordos. ¿Sabes dónde está la diferencia? Para cualquier cuadrado la proporción entre sus lados es 1. Los rectángulos pueden tener una propoprción cualquiera entre los lados desiguales.
     
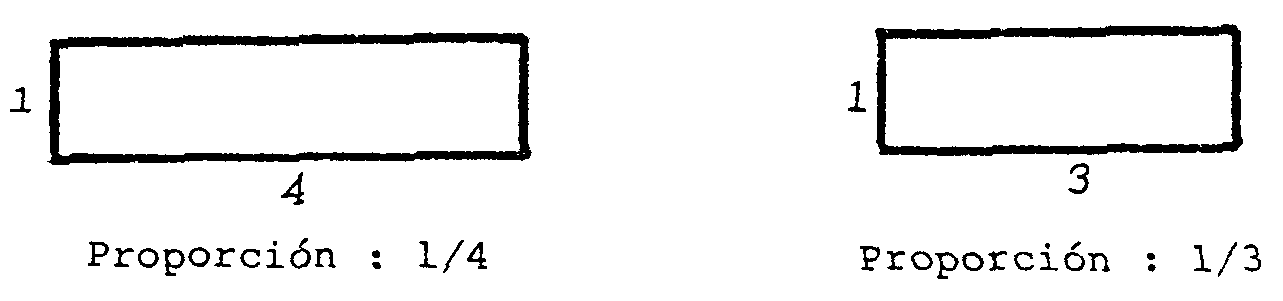
        Decir forma cuadrada es decir mucho. Decir forma rectangular es decir menos. Y menos aún es decir forma rectangular. Vamos a entretenernos con algunas formas rectangulares que aparecen en la vida nuestra de cada día.
 
        ¿De qué forma se debe cortar una hoja de papel? Parece que eso depende de lo que se pretenda hacer con ella. Está claro... pero una buena idea es cortar el papel en forma rectangular, naturalmente, pero de modo que al dividir en dos el rectángulo resulten dos rectángulos cuyos lados tengan la misma proporción entre sí que los del primitivo, es decir de tal modo que se conserve la forma. Así, si queremos partir estos dos rectángulos otra vez por la mitad, nos saldrán cuatro rectángulos de la misma forma exactamente, etc. Al partir en dos no nos salimos nunca de la misma forma de rectángulo. ¿Habrá algún rectángulo con esta curiosa propiedad?
 
        La hoja en la que escribí el borrador es, aproximadamente, de 21cm. x 29,7 cm. La proporción entre el lado mayor y menor es de 29,7/21=1,41.
Si divido la hoja por la mitad me salen dos hojas de 14,85cm. x 21 cm. y ahora la proporción es de 21/13,85=1,41.
Es curioso.
 
        Me han enviado un artículo en un tipo de hoja distinta de la mía. Voy a ver si tiene la misma propiedad. La hoja mide 21,5 cm. x 31,5 cm. La proporción es de 1,46. Si divido por la mitad me salen dos hojas de 15,75 x 21,5 y la proporción es 1,36. Así no tiene la misma propiedad que la primera, la mía. Sin embargo, si divido las que me han salido en último lugar por la mitad, me salen cuatro hojas de 10,75 x 15,75 y la proporción del lado mayor al menor es 1,46... ¡Igual que la hoja con la que empecé! ¿Es esto último de verdad muy sorprendente? Piensa un poco... En realidad lo que estoy comprobando es que
    Así no tiene nada de sorprendente, sucede para cualquier hoja rectangular, que al dividir dos veces resulte la misma proporción entre los lados. Pero sí que es algo especial que esta proporción se repita siempre.
 
        La hoja en la que yo escribo normalmente está hecha así con toda intención. El tamaño especial que tiene se llama DIN A-4. La del artículo que me han mandado es tamaño folio. Observa que en una hoja DIN A-4, sale el número 1,41. Tal vez te suene algo. El número es aproximadamente:  = 1,4142135... ¿Por qué? Piensa un poco.
 
        Tú quieres un rectángulo a x b tal que al cortar en dos (línea de puntos de la figura) resulten dos rectangulos con los lados en la misma proporción, es decir,  lado mayor /lado menor  debe resultar el mismo número en los rectángulos pequeños que en el grande. Así tendrá que ser     Por tanto b² = 2a² y así b/a = .
El misterio queda aclarado.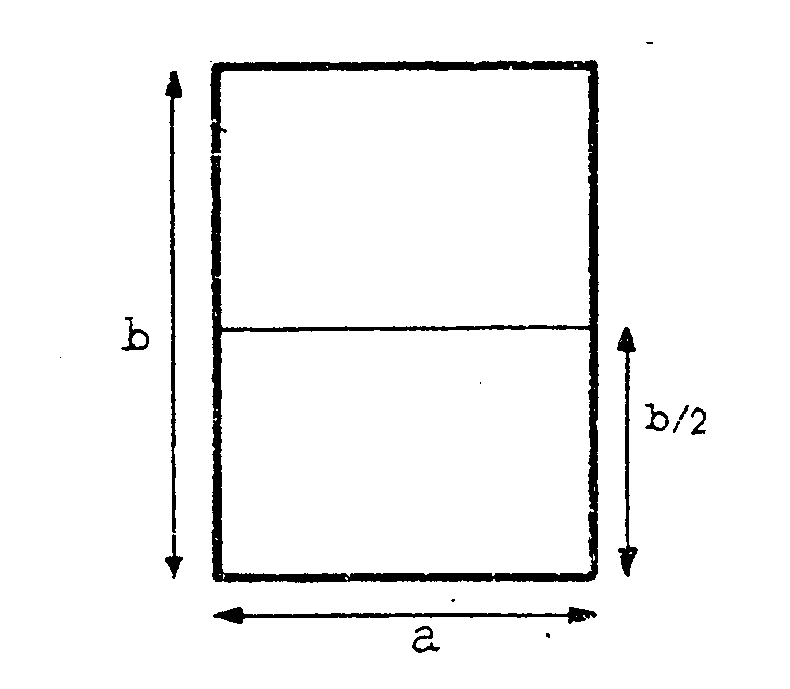                     
 
        Suponte que quisieras ahora una hoja rectangular con otra propiedad curiosa. Al quitarle un cuadrado, como se indica en el dibujo siguiente, debe quedar otro rectángulo con la mismísima forma del rectángulo original. ¿Cuál debe ser la proporción c/d para que esto pase? Mira al dibujo. Parece fácil ¿no?
 
        Tiene que ocurrir .  Así c² + cd-d² = 0 y por tanto , (  = 0,618033...)
        
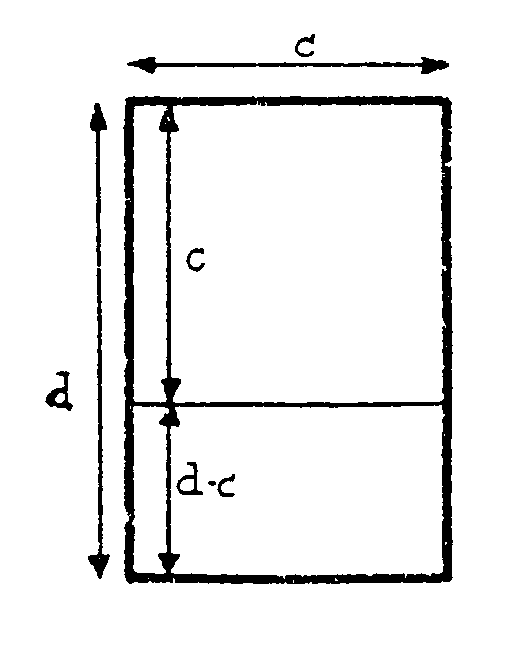
        Cuando dos longitudes se comportan como c y d, es decir, la longitud mayor, d, es a la menor, c, como ésta es a la diferencia, d-c, se dice que c es la sección áurea de d. Los griegos pensaban, no sin razón que un rectángulo con estas proporciones es particularmente agradable a la vista y los artistas griegos y posteriores han utilizado con profusión esta proporción áurea en la arquitectura, escultura, etc... El rectángulo así construído se suele llamar rectángulo áureo y el triángulo isósceles tal que los lados mayores son igulaes y el desigual, más pequeño, es sección áurea de ellos, se llama triángulo áureo. Nos lo encontramos más adelante en diversas circunstancias, así que más vale que aprendas a construir la sección áurea de un segmento dado.
 
        Por las cuentas que antes hemos hecho tú sabes que .
 
Esto te da una pista. ¿Cómo construyes  ? Observa que 
Con esto te será clara la construcción siguiente, si te dan d.
   
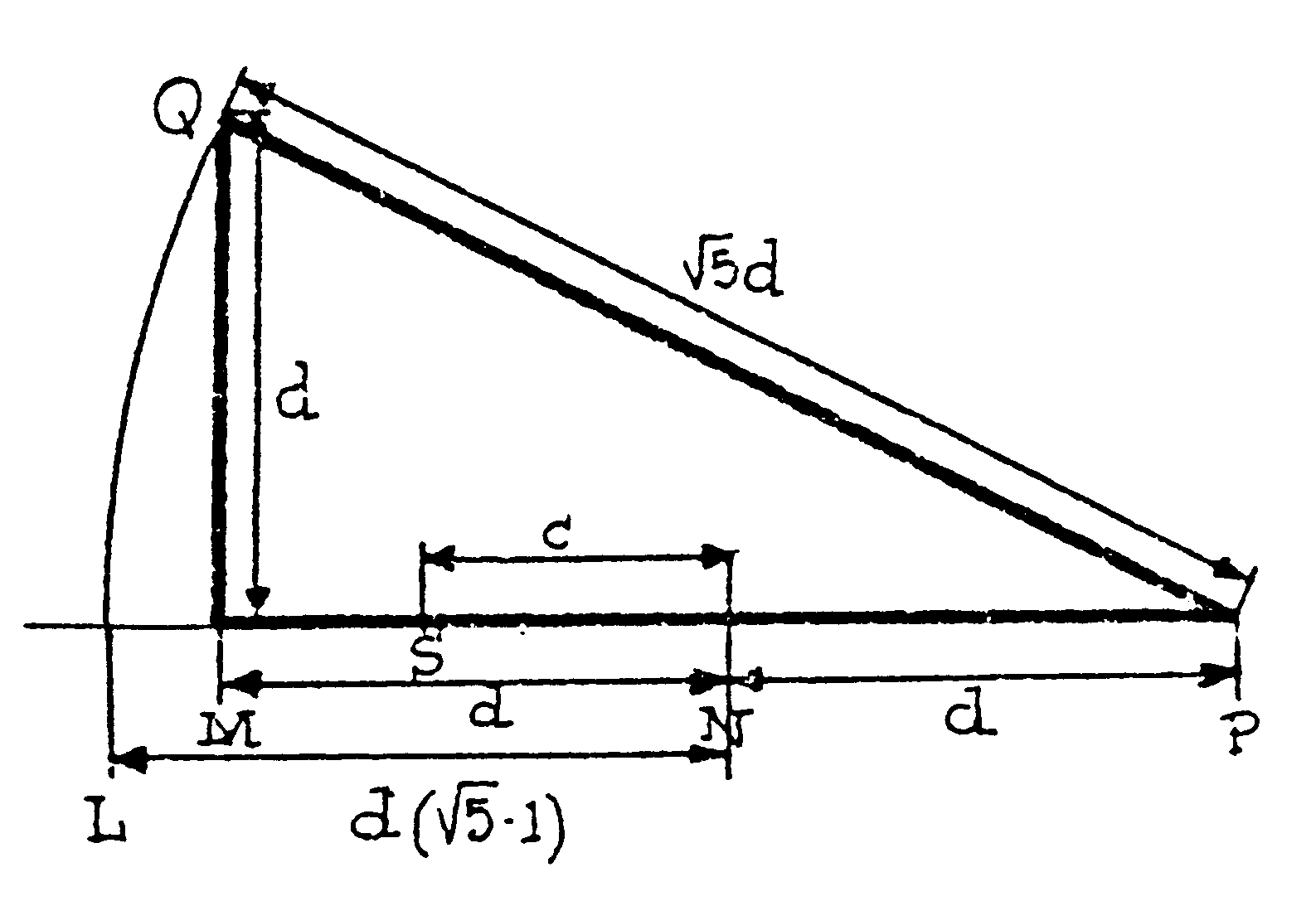
Si d es el segmento MN, lo prolongas otro tanto hasta P, levantas una perpendicular a MP en M y tomas Q tal que MQ = d. Entonces (Pitágoras) PG=. Con centro en P trazas el arco QL y así resulta claramente que
                                                                                                                           NS = 
 
        Hazte con unos cuantos rectángulos áureos y triángulos áureos y experimenta un poco con ellos sus áureas propiedades. El triángulo es aún más entretenido y original que el rectángulo. ¿Cuánto te parece que miden sus ángulos? ¿Qué le pasa si lo cortas a lo largo de la bisectriz de uno de los ángulos iguales?