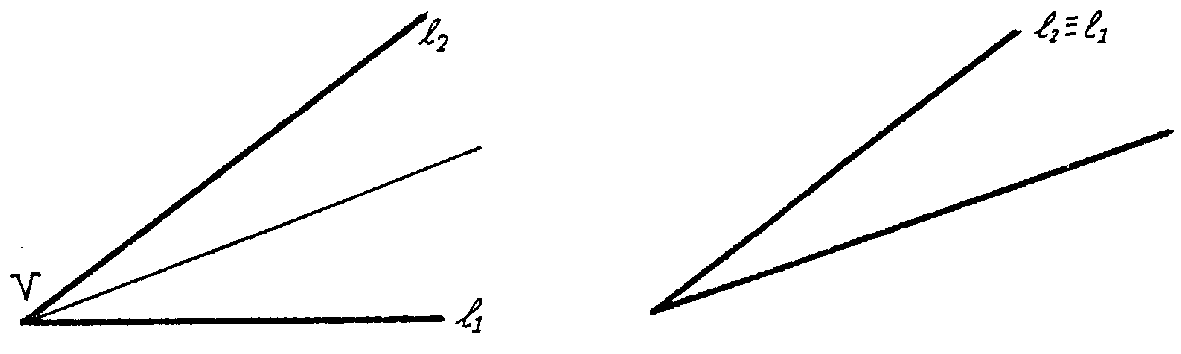GEOMETRIA DEL PLIEGUE             Euclides no tenía para sus clases en Alejandría la abundancia de papel que nosotros hoy disfrutamos. Pero seguro que de haber dispuesto de papel lo hubiera utilizado bien a fondo. ¿Qué se puede hacer plegando papel? Muchas cosas, como verás, y muy interesantes.
 
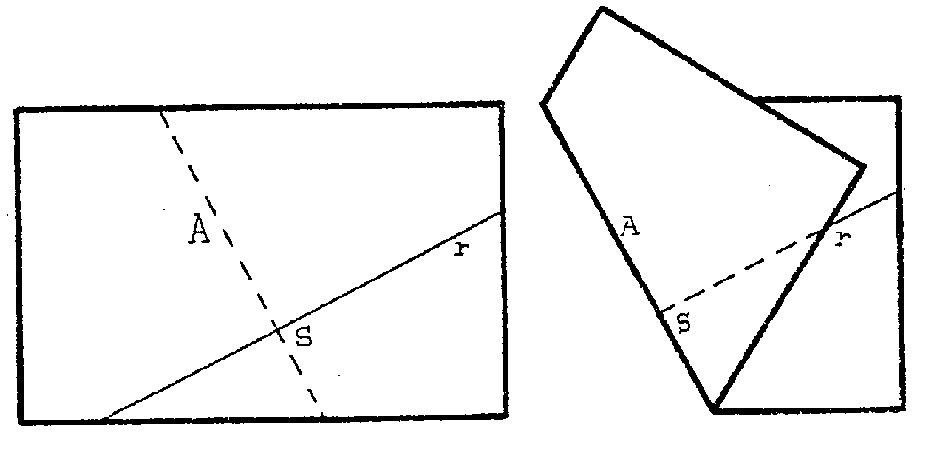
        Señala una recta en tu hoja, plegando el papel. Señala un punto cualquiera en el papel. ¿Cómo trazar la perpendicular por A a tu recta r? Muy fácil. Pliegas el papel de modo que el pliegue pase por A y que r venga a coincidir consigo misma, como indica la figura. Esto es fácil de conseguir haciendo intentonas y no plegando fuerte hasta que estés seguro de que al hacerlo va a suceder lo que tú quieres. Al desplegar el papel es claro que los ángulos en S son iguales y rectos, ¿no?
   
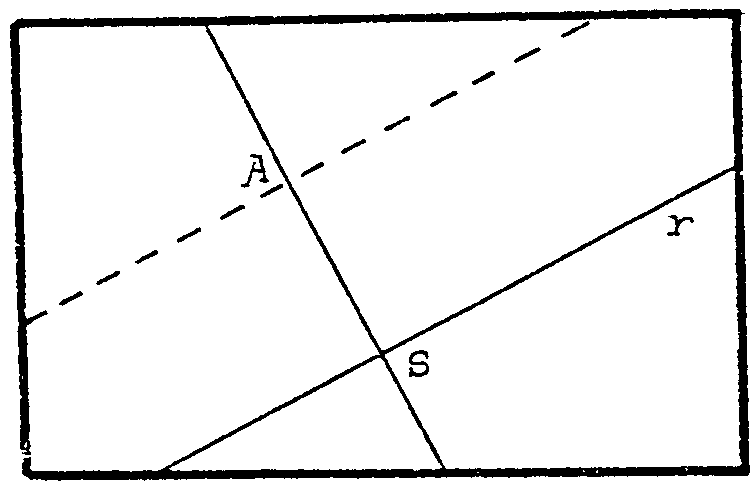
        ¿Cómo trazas una paralela por A a r? Ahora es fácil. Piensa... No tienes más que trazar una perpendicular por A a AS y ya la tienes, el pliegue que resulta es paralelo a r.
   
        Tienes dos puntos M y N en tu hoja. ¿Cómo vas a hallar el punto medio? Apenas tendrás que pensarlo. Pliegas por MN. Despliegas y luego pliegas de nuevo de modo que M coincida con N. Se forma un pliegue nuevo y la interesección de los dos pliegues te da el punto medio.
 
        Señala un ángulo en tu papel. ¿Cómo trazar la bisectriz? Está claro que sólo tienes que hacer un pliegue por elvértice V de modo que el lado l₁ vaya a coincidir con el otro l₂. El pliegue te da la bisectriz claramente.
      
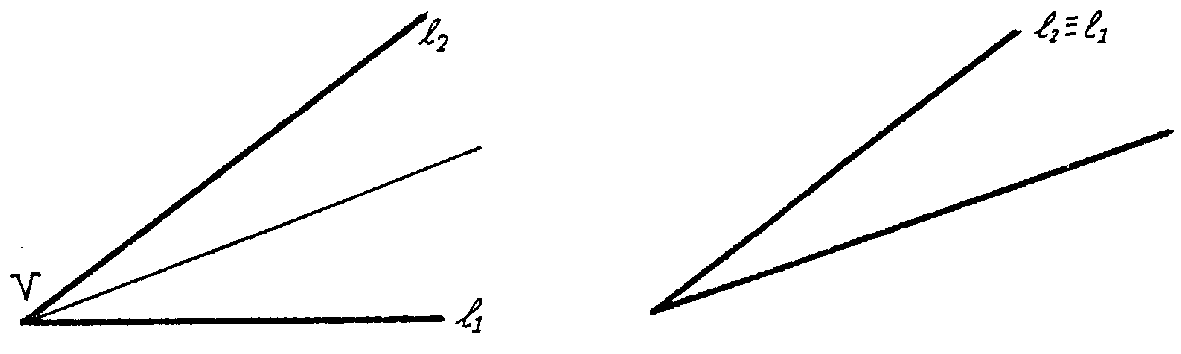
        Trazando la bisectriz ya sabes cómo dividir un ángulo en dos partes iguales, y repitiendo el proceso, en cuatro partes. Con el papel puedes resolver un problema famoso que a los griegos produjo muchos quebraderos de cabeza: dividir un ángulo dado en tres partes iguales. Inténtalo por tu cuenta. ¿Cómo lo harás en tu papel? Seguro que se te ocurre. Recortas el ángulo, formas un cucurucho, un cono cuyo vértice sea el del ángulo y ajustas los lados del ángulo de tal forma que al aplastar el cucurucho salgan dos pliegues que coincidan con los lados. Formar bien el cucurucho no es cosa del todo fácil. Debe proceder por intentonas, abriendo más o menos el cucurucho antes de aplastar para que se formen los pliegues adecuadamente como indican las figuras.
     
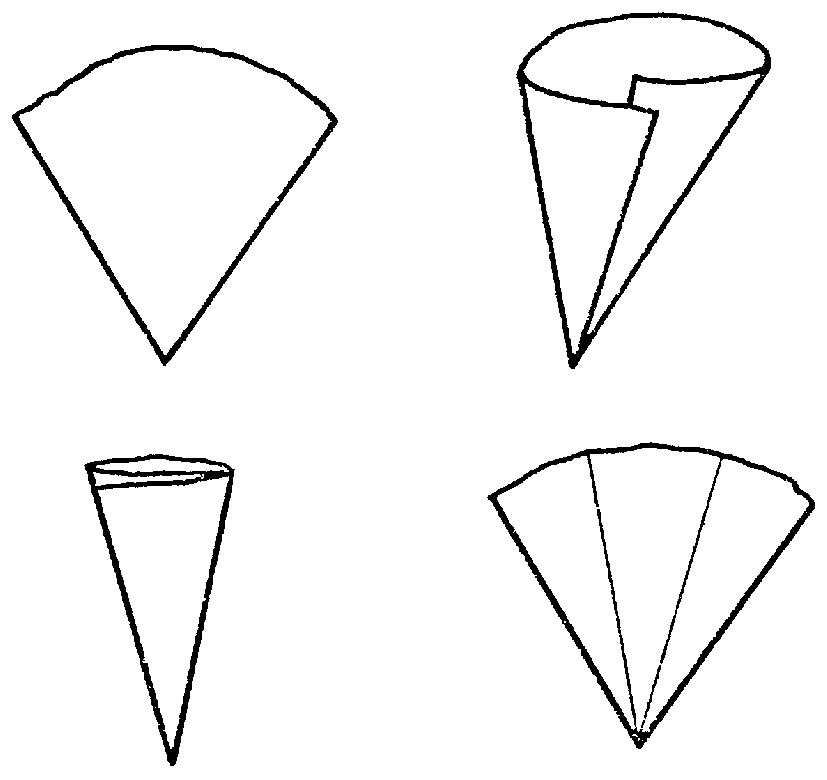
        Está bastante claro que si al aplastar has conseguido que los pliegues queden de esa manera, entonces al desplegar los tres ángulos formados son iguales y así has dividido el ángulo en tres partes iguales.
 
        Los griegos se construyeron instrumentos especiales para dividir un ángulo cualquiera en tres partes iguales. ¿Por qué no te haces uno tú mismo? Es muy fácil. En una cartulina recorta una figura con el patrón siguiente.
     
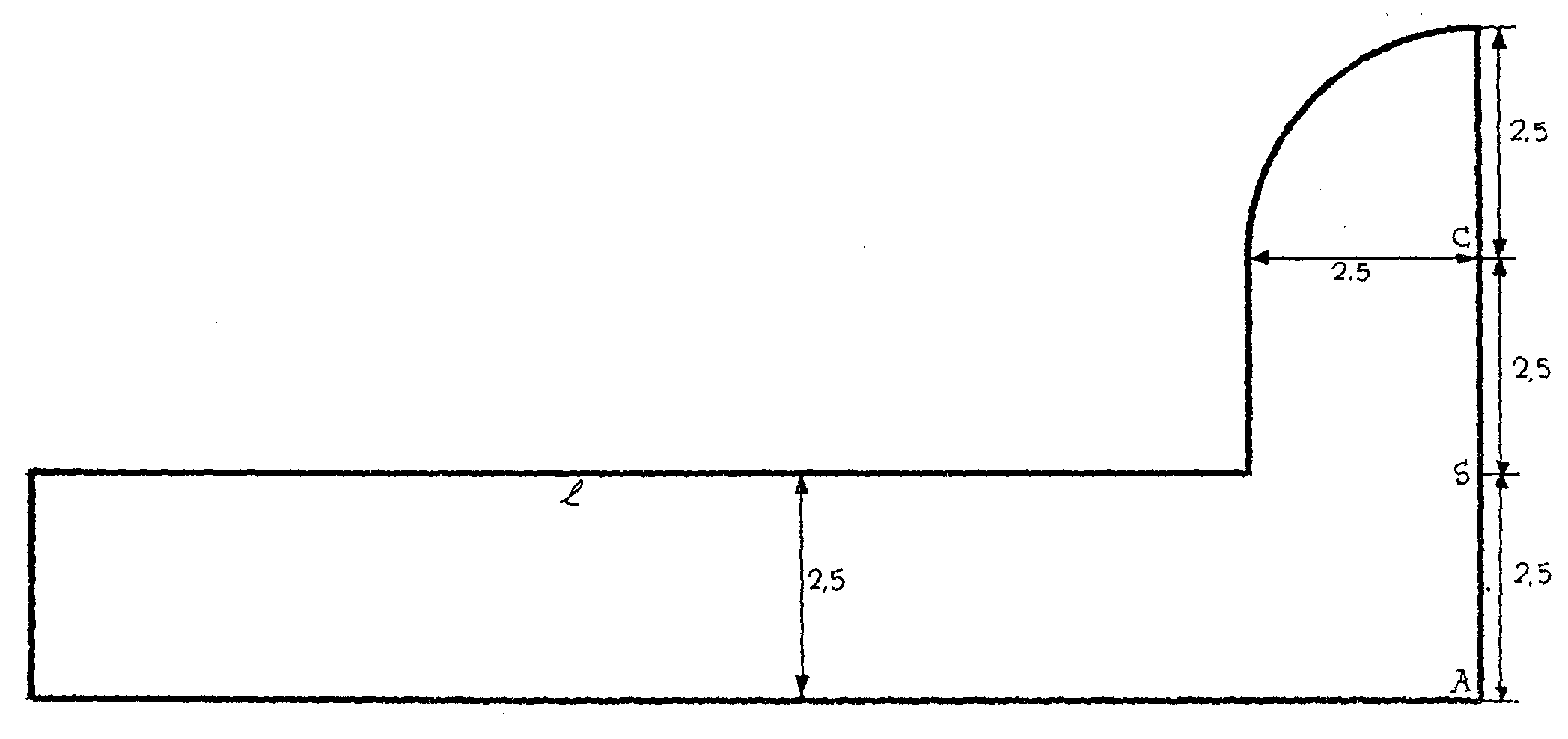
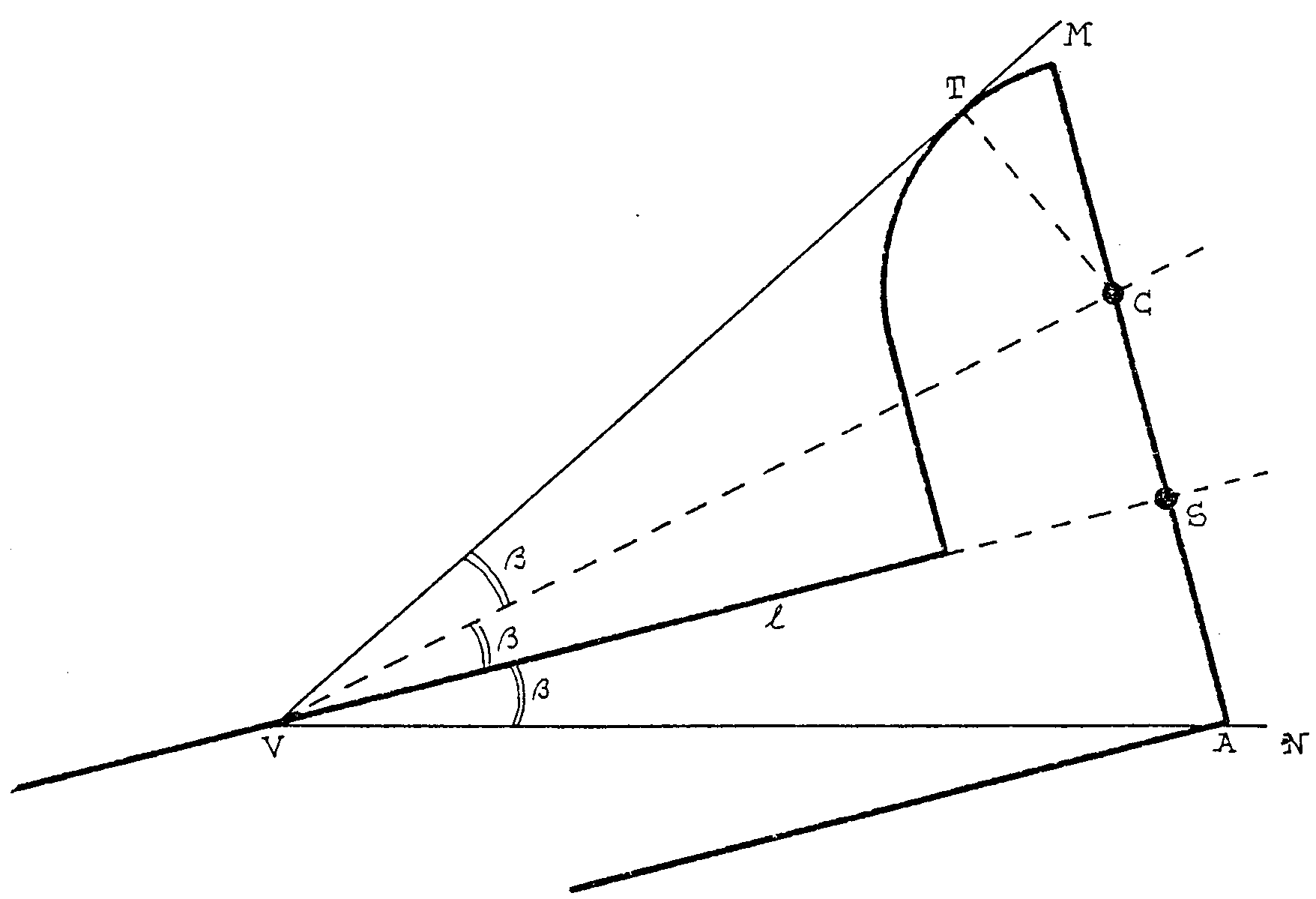
        Esta figura está construída como se indica. El arco de la punta es un arco de circunferencia con centro en C. Ahora si te dan un ángulo cualquiera como éste MVN, colocas tu instrumento como te indico, de modo que 1 pare por el vértice V, A esté sobre el lado inferiro del ángulo dado y el arco de circunferencia de arriba quede tangente al otro lado. Entonces señalas en el papel del ángulo de los puntos donde van a parar S y C. Si T es el punto de tangencia, te será muy fácil demostrar que los tres triángulos rectángulos VTC, VCS y VSA son iguales y así los tres ángulos señalados en V son iguales. Has dividido el ángulo dado en tres partes iguales.
     
        Los griegos del siglo III a. de C. conocieron este instrumento pero no les satisfacía. Querían una solución del problema de la trisección que no utilizara más que la regla y el compás de la forma normal. No lo sabían..., pero pedían demasiado. En el siglo XIX se logró demostrar que tal construcción es imposible. ¿Cómo? A grandes rasgos, se hizo así:
 
        El problema de dividir un ángulo cualquiera con regla y compás es equivalente al problema de construir con regla y compás un segmento cuya longitud es solución de una cierta ecuación de tercer grado a partir de segmentos de longitud igual a los coeficientes que aparecen en esta ecuación de tercer grado. Se observa a continuación que, con regla y compás, a partir de longitudes a₁, a₂, ..., a_n dadas sólo se puede construir segmentos cuya longitud se expresa mediante expresiones algebraicas (polinomios divididos por polinomios) de las longitudes dadas posiblemente junto con raíces cuadradas de tales expresiones. Se comprueba finalmente que la solución de la ecuación cúbica inicial no puede expresarse mediante ninguna expresión de este tipo. Así no se puede construir sólo con regla y compás.
 
        De esta misma forma se llegó a demostrar también que el famoso problema de Delfos (construir, sólo con regla y compás, un cubo de volumen doble que otro dado) era igualmente imposible.