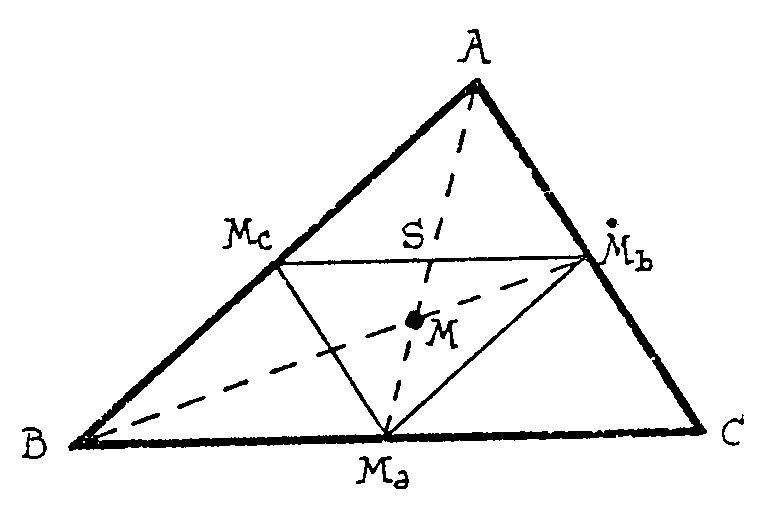Un poco de Geometría del Triángulo

UN POCO DE GEOMETRÍA DEL TRIÁNGULO Coge una cuartilla y unas tijeras. Recorta un triángulo bastante grande, que no sea demasiado regular, ni equilátero, ni isósceles, ni rectángulo... Algo parecido a éste pero en grande

Para no liarnos con los vértices, ponles letras A, B, C. Vamos a aprovechar lo que sabemos hacer plegando, para demostrar unas cuantas propiedades del triángulo. Traza la perpendicular a BC por A, es decir, la altura correspondiente al vértice A. El pie se va a llamar H_a. Pliega el triángulo por la mitad de la altura de modo que A vaya a coincidir con H_a. Así

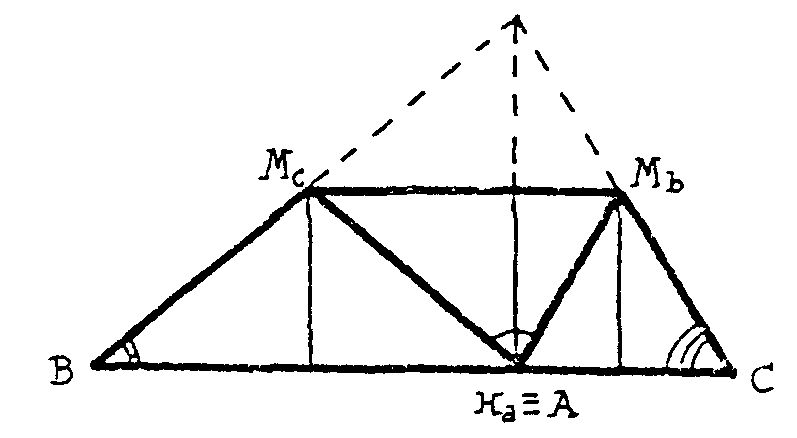
Ahora comprueba que puedes plegar por M_c de modo que B vaya a parar a H_a. ¿Podrías demostrar que efectivamente se tiene que poder plegar así? Sólo se trata de utilizar la igualdad de unos cuantos triángulos. Así te ha quedado

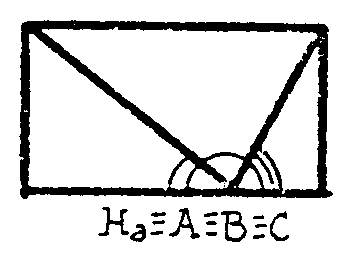
¿Qué observas? Los ángulos A,B,C, que han quedado ahora con sus vértices coincidiendo en Ha, suman claramente 180º y el área del triángulo ABC es el doble de la del rectángulo que has obtenido, es decir área triángulo ABC = 2 x base rectángulo x altura rectángulo = (1/2) base triángulo x altura triángulo No es un descubrimiento muy llamativo, pero vamos a seguir haciendo otros.

Recorta otro triángulo como el de antes para no armarte un lío con los pliegues que en él has hecho, porque ahora vamos a hacer muchos más y más interesantes. Traza con un pliegue la mediatriz correspondiente al lado BC. No tienes que hacer más que un pliegue que haga coincidir B con C. Traza del mismo modo las mediatrices de los otros dos lados. A mí me queda así

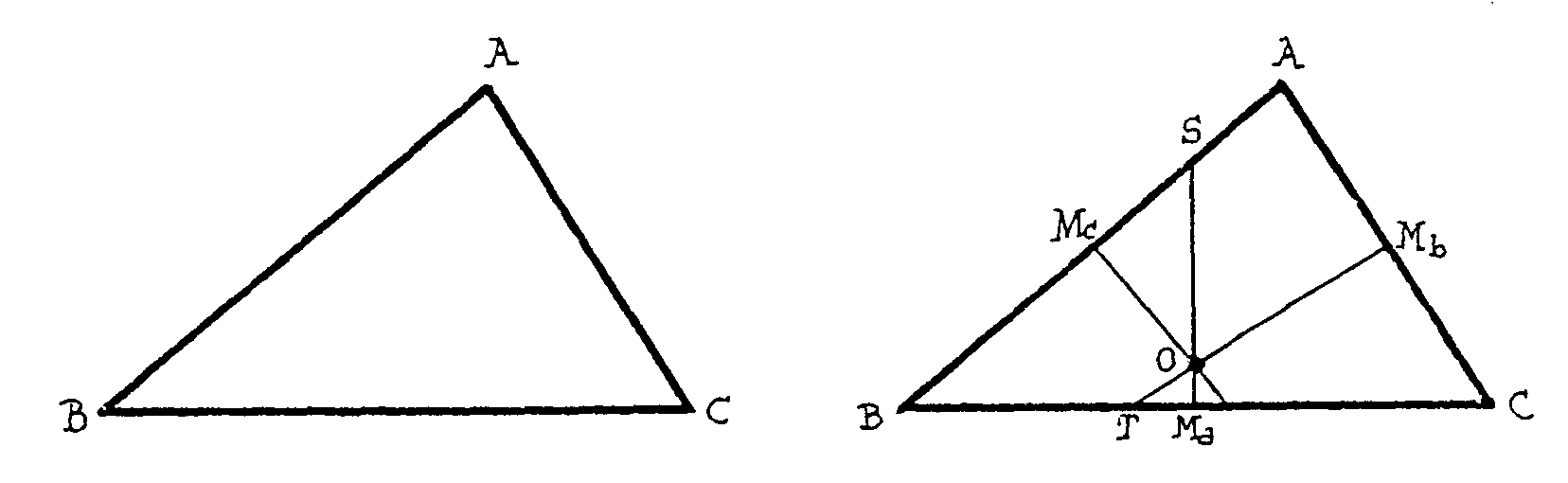
¿Qué observas?... ¡Las mediatrices se cortan en un punto! ¿Sabrías demostrar que esto no es una casualidad, que tenía que ser así? Recuerda: M_aS es mediatriz de BC. ¿Qué propiedad tienen todos sus puntos? Todos, como M_a, están a igual distancia de B que de C. Los de la mediatriz M_bT de AC están a la misma distancia de A que de C. Así el punto O, intersección de las dos mediatrices, está a igual distancia de los tres vértices. Pero si está a igual distancia de B que de A es que está sobre la mediatriz de AB. Por lo tanto, las tres mediatrices pasan por O y así queda resuelto el misterio. Además O está a la misma distancia de los tres vértices y es, por tanto, el centro de una circunferencia que pasa por A,B,C. ¿Tienes un compás a mano? ¡Compruébalo!

Vamos a seguir haciendo experimentos. Como ya tienes los puntos medios de los lados, que hemos llamado Ma, Mb y Mc, podemos, en el mismo triángulo, trazar las medianas fácilmente mediante pliegues. Pliega primero de modo que el pliegue contenga A y Ma, el pliegue que resulta es la mediana Ma. Pliega para obtener las otras dos. A mí me resulta algo así

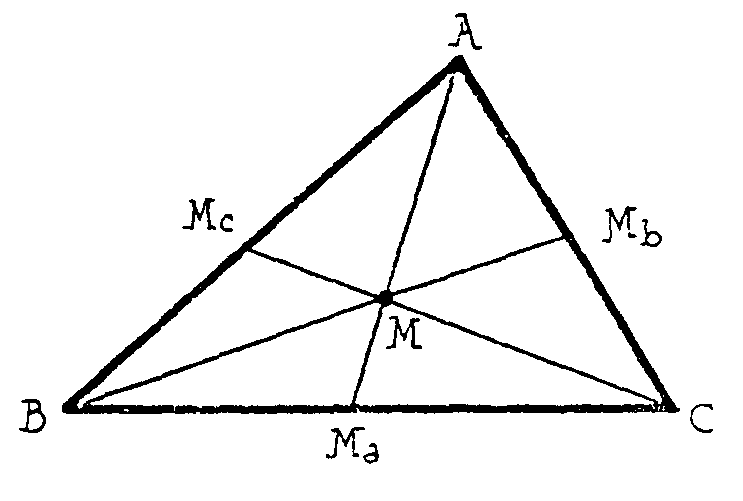
¿Qué observas?... ¡Las tres medianas se cortan en un punto! Llámalo M. Ese punto se suele llamar baricentro. Eso de bari tiene que ver con barómetro, con la presión y con el peso. Verás por qué. Alisa bien tu triángulo y recórtalo. Coloca tu lápiz vertical con la punta hacia arriba y sobre la punta de tu lápiz coloca tu triángulo horizontal de modo que M quede exactamente sobre la punta. ¡Tu triángulo queda en equilibrio horizontalmente sobre la punta de tu lápiz! (A menos que hayas hecho una chapuza horrible con los pliegues anteriores) El punto M es el único con esta propiedad, es el centro de gravedad de tu triángulo.

Plancha bien tu triángulo. Con la punta de tu lápiz bien afilado hazle un agujero cerca del vértice A y deja colgar el triángulo pinchado en él. Verás que la línea vertical que pasa por tu agujero viene a ser precisamente la que une el agujero al punto M. Lo mismo pasa con cualquier otro punto donde hagas el agujero. El punto M es el centro de todo el peso del triángulo. Sucede como si todo el triángulo tuviese concentrado su peso en el punto M. Por eso cuando pusiste el triángulo horizontal sobre tu lápiz con la punta en M, el triángulo no sabía hacia qué lado caerse y así se quedaba en equilibrio.

En tu triángulo ABC tienes ya muchos dobleces. Vamos a hacer unos cuantos más antes de mandarlo a la papelera. Pliega para trazar las tres alturas, como hicimos al principio. Así

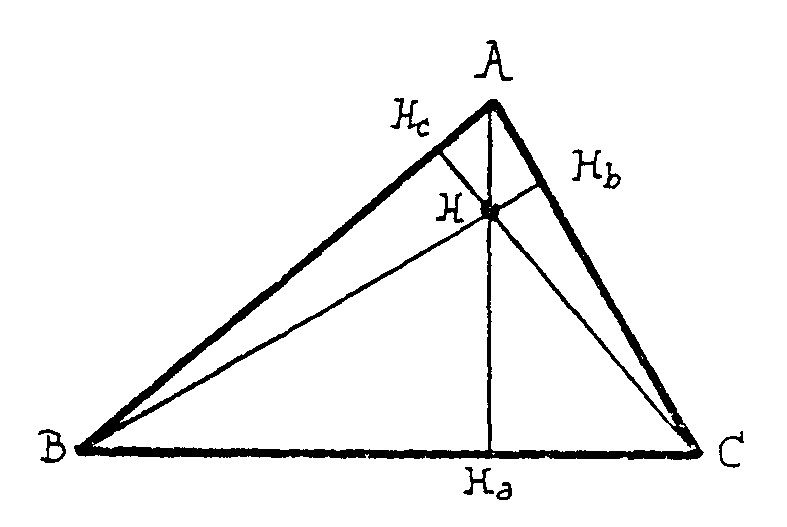
¡También las tres alturas se cortan en un punto! Vamos a llamar a ese punto H. Se denomina el ortocentro del triángulo. ¿Por qué tendrá que ser así? Con un poco de astucia resulta sencillo. Observa la figura siguiente obtenida trazando por A la paralela a BC, por B la paralela a AC y por C la paralela a AB.

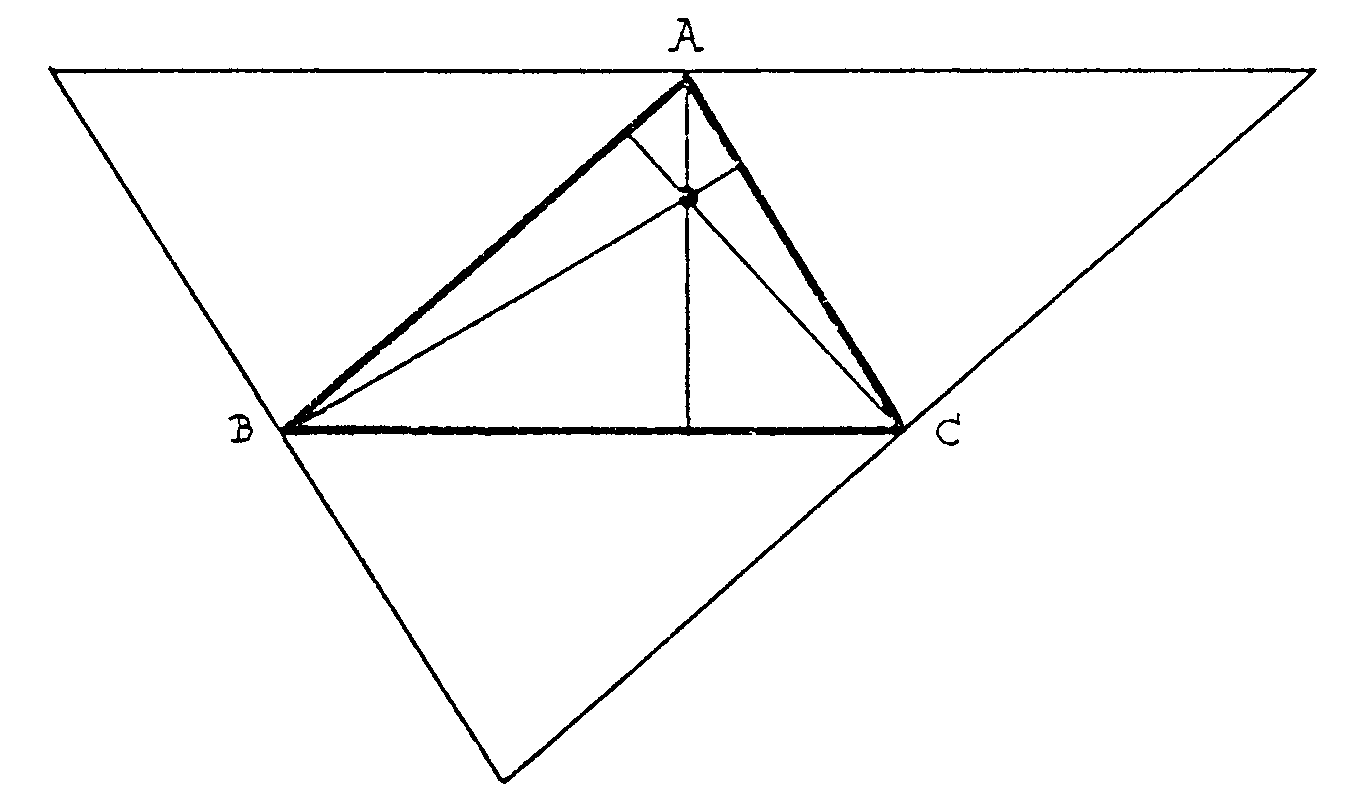
¿Qué observas?... Las alturas son las mediatrices de los lados del triángulo que ha resultado. Como las mediatrices de cualquier triángulo se cortan en un punto, nuestras alturas se cortan en un punto.

        Hemos obtenido tres puntos O (el circuncentro, centro de la circunferencia circunscrita al triángulo), M (baricentro) y H (ortocentro). ¿Cómo están dispuestos estos tres puntos? Pliega tu triángulo por MH. ¿Qué pasa? ¡El pliegue pasa también por O! Esa recta se llama la recta de Euler, que parece que fue quien primero descubrió esta propiedad de alineamiento de O, M y H.

        Si tienes por ahí una regla, haz unas cuantas medidas conmigo.
          - Mide MM_a
          - Mide M_aA
          - Mide MM_b y M_bB. Mide MM_c y M_cC.

        ¿Observas algo curioso? Probablemente no. Pues mira a ver si resulta M_aA = 2MM_a, M_bB = 2MM_b, M_cC = 2MM_c.

        Mide ahora OM y MH y observa que MH = 20M.

        Todos estos misterios se aclaran fácilmente con lo que probablemente sabes sobre triángulos semejantes y homotéticos. Fíjate en la figura siguiente

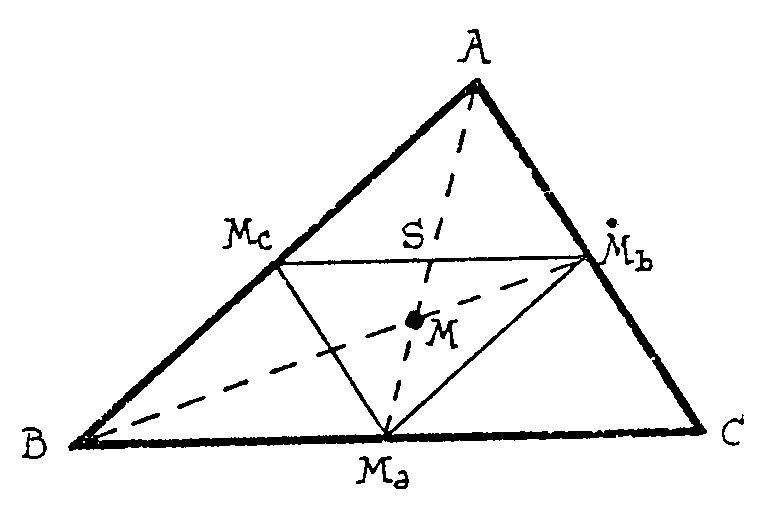
Fácilmente podrás comprobar que M_cMb es paralelo a BC y M_cM_b es paralelo a BC y M_cM_b = 1/2 BC. Lo mismo sucede con los otros lados del triángulo pequeño M_aM_bM_c.

Como M_aS es la medianta de M_aM_bM_c correspondiente a M_a, resulta que M_aS= 1/2 AM_a y MS = 1/2 MM_a (M es el punto donde se cortan BM_b y AM_a). Así resulta fácilmente MM_a = 2MS y por tanto (segmentos correspondientes en el triángulo grande ABC) MA = 2 MM_a. Así resulta que MM_b corta a AM_a en M que está a doble distancia de A que de M_a. Haciendo lo mismo con M_cC, resulta que CM_c corta también a AM_a en un punto que está a doble distancia de A que de M_a, es decir, corta a AM_a en el mismo M de antes. Por tanto, las tres medianas se cortan en un punto M. Hemos demostrado con esto lo que antes habíamos comprobado con nuestros pliegues.