radianes.
En este caso tenemos un cuadrado por lo que las espirales equiangulares serán de
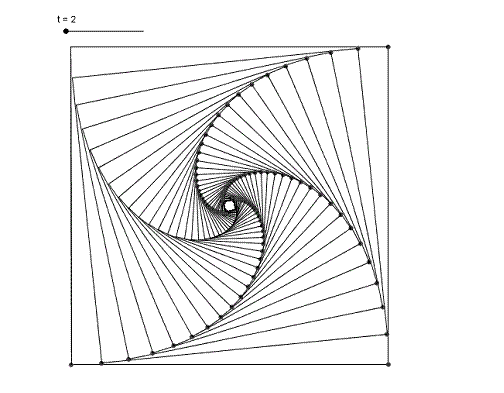
π/4 radianes.Modelo 4 insectos
Hemos
explicado que si tenemos un polígono regular de n caras el rastro que dejan los
insectos son espirales equiangulares de
radianes.
En este caso tenemos un cuadrado por lo que las espirales equiangulares serán de
π/4 radianes.
El método para la construcción es idéntico al del modelo de 3 insectos por lo que sólo escribiremos las ecuaciones de las espirales.
Empecemos por el primer insecto, situado en el punto A. Tendrá de ecuaciones
A= (e^(t / tan(π / 4)) cos(t), -1 e^(t / tan(π / 4)) sin(t))
* Los signos de las ecuaciones paramétricas dependen de la orientación que le damos a la espiral según el vértice en el que se encuentre el insecto.
En este caso hemos seleccionado el punto (1,0) como el centro del cuadrado, es decir, el punto final de la trayectoria que describe el insecto ya que éste recorrerá la espiral de fuera hacia adentro.
A continuación situaremos el punto B. Deberemos rotarla espiral anterior π/2. Éste es el ángulo formado por los segmentos que unen el centro con dos vértices consecutivos del cuadrado.
Después del ajuste nos queda la siguiente ecuación:
B= (-1 e^(t / tan(π / 4)) cos(t + π / 2) + 1, e^(t / tan(π / 4)) sin(t + π / 2) - 1)
Realizamos el mismo proceso con C y D obteniendo:
C= (-1 e^(t / tan(π / 4)) cos(t - π / 2) + 1, e^(t / tan(π / 4)) sin(t - π / 2) + 1)
D= (-1 e^(t / tan(π / 4)) cos(t) + 2, e^(t / tan(π / 4)) sin(t))
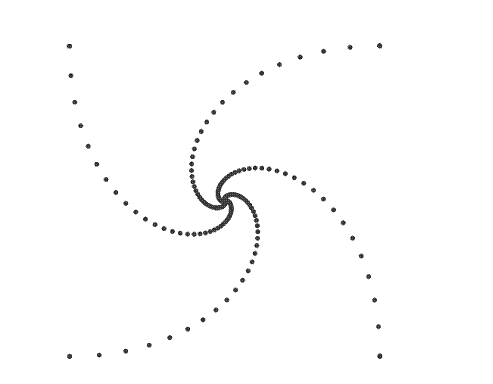
Si queremos mostrar las líneas de dirección de cada insecto construimos los segmentos AB, BC y CA.
Podemos apreciar que cada línea es tangente a los espirales y forma parte un polígono semejante al original, luego, la espiral formada debe ser una equiangular.
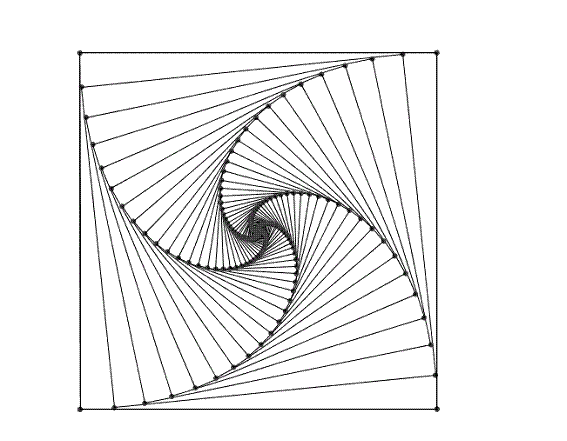
Podemos aumentar el valor del extremo inferior del deslizador para que no lleguen a encontrarse en nuestro dibujo y quede en blanco el centro del triángulo.
