Clase 11 enero 2001
Clase 18 enero 2001

Poncelet
El teorema principal:

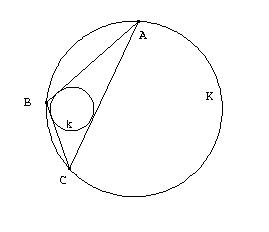Dos circunferencias, una k dentro de otra K.
Para un punto A de K sucede lo siguiente:
Trazamos por A una tangente a k que vuelve a cortar a K en B; por B trazamos la otra tangente a k, que vuelve a cortar a K en C; por C trazamos la otra tangente a k, que resulta que vuelve a cortar a K en A (es decir, se cierra la sucesión de tres tangentes).
 
 
 

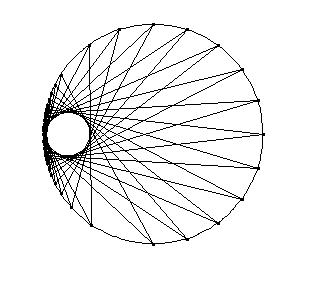Entonces eso mismo pasa (es decir el triángulo también se cierra) cuando hacemos la misma operación partiendo de cualquier otro punto A* de K.

El teorema general substituye el 3 del teorema anterior por n. Es decir, si el n-ágono se cierra partiendo de un punto se cierra partiendo de cualquier otro.

Más general aún. Vale para cualquier par de cónicas...

También se le suele llamar el teorema del polígono cerrado de Poncelet. (Poncelet's closure theorem)

Un teorema semejante de Steiner relativamente fácil.

Dos circunferencias K y k, una dentro de la otra, admiten una cadena de n circunferencias cada una tangente interioremente a K y exteriormente a k y a otras dos de la cadena. Entonces, partiendo de una circunferencia cualquiera tangente a K y k existe otra cadena de n circunferencias como la anterior.

La clave: una inversión  puede transformar dos círcunferencias que no se cortan en dos circunferencias concéntricas. Lo mismo se puede hacer mediante una proyección estereográfica. Demostración.

Demostración del teorema de las cadenas de circunferencias de Steiner

Para el teorema de Poncelet,
¿Existirá alguna demostración sintética sencilla semejante?

Una demostración del caso n=3 sencilla, mediante un teorema que resulta ser equivalente:

Tres circunferencia de igual radio r pasan por un punto O. Entonces los otros tres puntos de intersección de cada dos circunferencias distintos de O están en una circunferencia G también de radio r.

Además, si tomamos un punto cualquiera A de G, trazamos una circunferencia de radio r que pasa por A y O y corta a G en B, por B y O trazamos otra circunferencia de radio r que corta a G en C y por C y O otra de radio r, entonces ésta vuelve a cortar G en A. Es decir la cadena de las 3 circunferencias se cierra.

Más detalles

¿Y para n mayor?

El cubo en cuatro dimensiones (versión 1).
El cubo en cuatro dimensiones (versión 2).
El cubo en cuatro dimensiones en movimiento.

Una forma de explicar el tipo de demostración algebraica del teorema de Poncelet (la de los cuadernos de Saratov).

Consideramos una recta, por ejemplo Ox. Tomamos un punto (t,0) de ella. Trazamos una recta por él de pendiente m y la intersecamos con y=a y nos da un punto, nos desplazamos por y=a una distancia d a la derecha y hacia arriba. Trazamos por el punto así obtenido una recta de pendiente n. Corta a Ox en un punto (f(t,a,m,n,d),0). Imponemos que sea t=f(t,a,m,n,d). Es claro que resulta una condición entre a,m,n,d. Si se cumple, entonces se cumple para cualquier t.

Una sencilla muestra con DERIVE

Esto es lo que se hace en el teorema de Poncelet.

Lo que ahora sucede sucede es que resulta x₁(t,a,r,R)=x₂(t,a,r,R), y₁(t,a,r,R)=y₂(t,a,r,R), siendo (x_1,y₁₎ y (x_2,y₂) los puntos inicial y final de la cadena de segmentos tangentes, R y r los radios de los círculos y a la distancia entre sus centros.

Eliminamos la t entre las dos ecuaciones, es decir suponemos que para un t general se verifica el cierre, y así  si se da esta relación entre R,r,a, se verifica para todo t. Es decir, si se verifica el cierre para un punto se verifica para todos.

Algunas tentativas con DERIVE en torno al teorema de Poncelet.

La relacion de Chappel y las generalizaciones para n=4,5,6,... son precisamente estas relaciones.