Ya desde los Babilónicos (2000 a.C. – 600 a.C.) la noción de función estaba vigente entre los matemáticos, éstos, utilizaban tablillas para sus cálculos astronómicos; estas tablillas estaban dispuestas en dos columnas, de forma similar a nuestras tablas de valores que acostumbramos a construir para nuestras funciones. Aunque utilizasen la noción de función, esta no estaba definida aún como lo está en nuestros días. Han tenido que pasar muchos siglos hasta llegar al concepto que tenemos hoy.
No fue hasta el siglo XIV, cuando Nicolás de Oresme (1320-1382) tuvo una brillante idea y la noción de función volvió a resurgir. A Nicolás de Oresme se le ocurrió dibujar gráficamente el modo en que las cosas variaban, pero estas representaciones no eran fieles a la realidad, no las podemos tomar como la dependencia entre variables que actualmente conocemos.
La gran contribución de Galileo (1564-1642) fue la representación de gráficas basadas en la experiencia y la medida, su gran empeño por obtener resultados exactos en el estudio de los movimientos le llevó a la necesidad del concepto de variable dependiente.
Ya en el siglo XVII, la evolución del álgebra permitió a Fermat y Descartes el descubrimiento de la Representación Analítica gracias al avance del análisis. Pero no fue hasta finales de dicho siglo que Leibniz y Bernoulli definen el concepto de función como lo conocemos en nuestros días, en un artículo de Bernoulli de 1718 aparecía:
“llamamos función de una magnitud variable a una cantidad compuesta de cualquier manera que sea de esta magnitud variable y de constantes”
En este mismo artículo, empieza a nombrar a la función por la letra f.
En 1755, Euler da una noción más abstracta y universal de función:
“Si ciertas cantidades dependen de otras cantidades de tal manera que si las otras cambian, estas cantidades cambian también, entonces, tenemos la costumbre de nombrar estas cantidades funciones de estas últimas; esta denominación es la más extensa y contiene en ella misma todas las formas por las cuales una cantidad puede ser determinada por otras. Por consiguiente, si x designa una cantidad variable, entonces todas las otras cantidades que dependen de x, no importa de qué manera, son llamadas funciones de x”.
Como estos matemáticos nombrados anteriormente, ha habido muchos después de ellos que han dado más definiciones de la noción de función, como Cauchy, Dirichlet, Riemann, las cuales han sido más formales cada vez, hasta llegar a la actualidad, donde el concepto de función se asocia al de aplicación entre conjuntos.
f es una función de
si a cada número real x є D, le hace corresponder
otro número real f(x):
Para que la función esté bien definida se debe cumplir que para cada valor x є D, el valor f(x) es único.
Por ejemplo, la primera de las siguientes gráficas NO corresponde a una función, mientras que la segunda sí:
Se llama dominio de definición de una función f, Dom f, al conjunto de valores de x, para los cuales existe la función, es decir:
Dom f = { x є R / f(x) está bien definida }
Se llama recorrido de una función f, Im f, al conjunto de valores de f(x), tales que x pertenece al dominio de f, es decir:
Im f = { f(x) є R / x є Dom f }
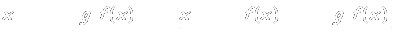Dadas
dos funciones f y g, tales que Im f
c
Dom g, denominamos función compuesta de f y g,
g◦f,
a la función
g◦f
se lee al revés de como se escribe, es decir “f compuesta con g” ya que f es la
primera función que actúa sobre x.
Por ejemplo, si tenemos las funciones
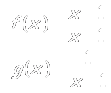
la composición g◦f es
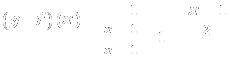
Llamamos función inversa de f,, a aquella función que verifica las siguientes relaciones,
Existe
inversa, si para cada x del dominio existe un único valor f(x) (a esto es la
inyectividad)
A
la hora de representar gráficamente la función f y su inversa, comprobaremos que
estas son simétricas respecto la recta y=x
Por ejemplo, f(x)=Ln(x) es la función inversa de g(x)=ex
Se dice que una función es par si es simétrica respecto del eje OY, es decir, si verifica que f(x) = f(-x).
Se dice que es impar si es simétrica respecto del origen de coordenadas, es decir, si verifica que f(x) = -f(-x)
Una función f es periódica si existe un número real k tal que f(x)=f(x+k) para todo x perteneciente al dominio de f.
Una asíntota es una recta a la que se aproxima considerablemente la gráfica de una función sin llegar a tocarla nunca.
Tipos de asíntotas:
Las asíntotas horizontales y oblicuas son excluyentes; es decir, la existencia de unas, implica la no existencia de las otras.
Decimos que una función f es continua en a є Dom f, si se verifica:
Si una función no cumple lo anterior, decimos que presenta una discontinuidad en el punto a. El siguiente esquema muestra los posibles tipos de discontinuidades que puede presentar una función:
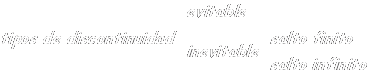
Discontinuidad evitable
Como puedes apreciar en el dibujo, este tipo de discontinuidades se pueden "evitar " definiendo una nueva función g del siguiente modo:
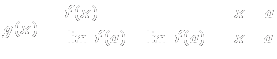
de manera que la función así definida es continua.
Puede darse el caso en el que f(a) no esté bien definida; en dicho caso se procede de la misma manera.
Discontinuidad inevitable
De salto finito
De salto infinito
Estudiando el signo de la derivada de una función f, podemos determinar los intervalos de crecimiento y decrecimiento del siguiente modo:
No hemos considerado el caso f'(x)=0, que se estudiará en el siguiente apartado.
Se dice que a є Dom f es un punto singular de la función f si su tangente a la curva es horizontal (punto de tangente horizontal).
Distinguimos tres casos:
Estudiando el signo de la segunda derivada de una función f, podemos determinar los intervalos de concavidad y convexidad del siguiente modo:
El cambio de concavidad/convexidad viene determinado por un punto de inflexión.
Hay veces en que resulta útil averiguar el área bajo la gráfica de una función.
Dicha área es el resultado de calcular la integral entre a y b de f
Recuerda que por la regla de Barrow, si F es una primitiva de f:
Para calcular el área comprendida entre la curva y=f(x), el eje OX y las abscisas x=a, x=b, hacemos lo siguiente:
Calculamos los puntos de corte de f(x) con el eje OX y seleccionamos los comprendidos entre a y b: x1, x2, ... xn .
Hallamos F(x), primitiva de f(x).
Área = |F(x1) - F(a)| + |F(x2) - F(x1)| + ... + |F(b) - F(xn)|
Para calcular el área encerrada entre dos curvas y=f(x), y=g(x), hacemos:
Hallamos una primitiva H de la función diferencia h(x)=f(x)-g(x).
Calculamos los puntos de corte de h(x) con el eje OX, x1, x2, ... xn .
Área = |H(x2) - H(x1)| + |H(x3) - H(x2)| + ... + |H(xn) - H(xn-1)|
Normalmente, una tabla de valores no es herramienta suficiente para poder representar gráficamente una función. Las propiedades vistas anteriormente nos ayudarán a dibujar la gráfica de cualquier función.
Los pasos a seguir para representar gráficamente una función f son los siguientes:
Conocer Dom f e Im f .
Estudiar si f tiene asíntotas y
dibujarlas. Si no tiene asíntota horizontal ver si
Estudiar la paridad y periodicidad de f.
Hallar los puntos de corte con los ejes.
A partir de f' y f'' estudiar la monotonía, curvatura, máximos, mínimos y puntos de inflexión.
Veamos, por ejemplo, cómo representar la función
Dom f =
Im
f =
x=1 es asíntota vertical por ser
No tiene asíntota horizontal, por ser
y=x+2 es asíntota oblicua, por ser
si
la diferencia
es f(x)-y>0, lo que significa que la curva se aproxima a la asíntota por
encima en +∞. Si
la diferencia es
f(x)-y< 0, lo que significa que la curva se aproxima a la asíntota por
debajo en -∞.
f'(x)=0 para x=0 y x=3
f es creciente en (-∞,1)U(3,+∞) y decreciente en (1,3), por tanto, (3,f(3))=(3,27/4) es un mínimo.
f'(x)=0 para x=0
f es convexa en (-∞,0) y cóncava en (0,1)U(1,+∞), por tanto, (0,f(0))=(0,0) es un punto de inflexión.
Estas funciones surgen con el fin de caracterizar ángulos.
Seno: y=sen(x)
Coseno: y=cos(x)
Las funciones y=sen(x), y=cos(x) son continuas y periódicas. Ambas tienen infinitos puntos de corte con el eje OX e infinitos puntos de tangente horizontal. Su recorrido es [-1, 1]. No tienen asíntotas ni ramas infinitas.
Tangente: y=tg(x)
La función y=tg(x)
no es continua y tiene asíntotas verticales en los puntos
1. Sean f y g dos funciones invertibles, ¿Es (g◦f)-1 = g-1◦f-1? ¿O bien, (g◦f)-1 = f-1◦g-1?
tienen la
misma representación gráfica? ¿Por qué?
3. Si f es una función polinómica tal que para todo x es f(x2+1)=x4+5x2+3, entonces ¿Cuánto vale f(x2-1)?
4. Si f(x) es una función definida
por
siendo
a>0 y
,
¿Cuánto vale a?
5. Si
es
igual a:
a) -f(x) b) 2f(x) c) 3f(x) d) [f(x)]2 e) [f(x)]2-f(x)
6. Una de las siguientes funciones es par, ¿Cuál?
a) y=x2+x b) y=x3 c) y=xcos(x) d) y=xsen(x) e) y=x2sen(x)
7.
¿Cuál es el intervalo
definido por el conjunto 
?
8.
¿Cuántas asíntotas tiene la
función
?
9. Representa gráficamente la siguiente función, para ello ayúdate de sus propiedades.
10. A partir de la gráfica de f’(x) deduce información para representar aproximadamente f(x).
